5230. Синус угла при основании равнобедренного треугольника равен \frac{8}{17}
, а основание равно 60. Внутри треугольника расположены две равные касающиеся окружности, каждая из которых касается двух сторон треугольника. Найдите радиусы окружностей.
Ответ. 6
или 5\frac{10}{49}
.
Решение. Первый способ. Рассмотрим равнобедренный треугольник ABC
, в котором \sin\angle ABC=\frac{8}{17}
, BC=60
. Пусть AH
— высота треугольника ABC
. Тогда H
— середина BC
. Обозначим \angle ABC=\angle ACB=\alpha\lt90^{\circ}
(угол при основании равнобедренного треугольника — острый). Тогда
\cos\alpha=\sqrt{1-\left(\frac{8}{17}\right)^{2}}=\frac{15}{17},~\tg\alpha=\frac{8}{15},~AB=\frac{BH}{\cos\alpha}=\frac{30}{\frac{15}{17}}=34.
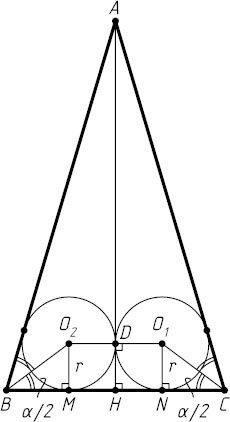
Предположим, что окружность радиуса r
с центром O_{1}
вписана в угол ACB
и касается основания BC
в точке N
, а окружность того же радиуса с центром O_{2}
вписана в угол ABC
, касается первой окружности, а также основания BC
— в точке M
(рис. 1).
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому \angle ABH=\frac{\alpha}{2}
,
\tg\frac{\alpha}{2}=\frac{\sin\alpha}{1+\cos\alpha}=\frac{\frac{8}{17}}{1+\frac{15}{17}}=\frac{1}{4}.
Из прямоугольного треугольника BMO_{2}
находим, что
BM=O_{2}M\ctg\angle MBO_{2}=r\ctg\frac{\alpha}{2}=4r.
Тогда CN=BM=4r
.
Линия центров касающихся окружностей проходит через точку их касания, поэтому O_{1}O_{2}=2r
, а так как O_{1}O_{2}MN
— прямоугольник, то MN=O_{1}O_{2}=2r
. Следовательно,
60=BC=BM+MN+CN=4r+2r+4r=10r,
откуда находим, что r=6
.
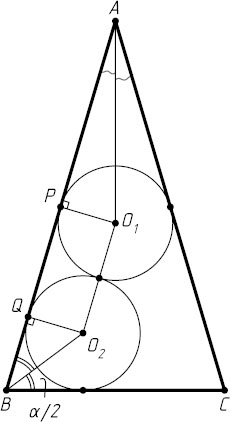
Пусть теперь окружность радиуса r
с центром O_{1}
вписана в угол BAC
и касается боковой стороны AB
в точке P
, вторая окружность радиуса r
с центром O_{2}
вписана в угол ABC
, касается боковой стороны AB
в точке Q
, а также касается первой окружности (рис. 2).
Из прямоугольных треугольников APO_{1}
и BQO_{2}
находим, что
AP=O_{1}P\tg\angle AO_{1}P=r\tg\alpha=\frac{8}{15}r,
BQ=O_{2}Q\ctg\angle QBO_{2}=r\ctg\frac{\alpha}{2}=4r.
Следовательно,
34=AB=AP+PQ+QB=AP+O_{1}O_{2}+QB=\frac{8}{15}r+2r+4r=\frac{98}{15}r,
откуда находим, что r=\frac{255}{49}=5\frac{10}{49}
.
В случае, когда окружности вписаны в углы BAC
и ACB
, получим тот же результат.
Второй способ. Рассмотрим равнобедренный треугольник ABC
, в котором AC=AB
, BC=60
, \sin\angle ABC=\frac{8}{17}
. Пусть AH
— его высота. Тогда \cos\angle ABC=\frac{15}{17}
,
AC=AB=\frac{BH}{\cos\angle ABC}=\frac{30}{\frac{15}{17}}=34,
S_{\triangle ABC}=\frac{1}{2}AB\cdot BC\sin\angle ABC=\frac{1}{2}\cdot34\cdot60\cdot\frac{8}{17}=480.
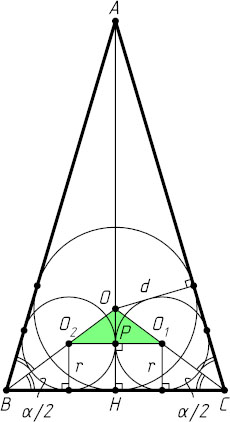
Предположим, что окружность радиуса r
с центром O_{1}
вписана в угол ACB
, а окружность того же радиуса с центром O_{2}
вписана в угол ABC
и касается первой окружности (рис. 3).
Центр окружности, вписанной в угол, лежит на его биссектрисе, поэтому лучи BO_{1}
и CO_{2}
— биссектрисы углов треугольника. Точка их пересечения O
— центр окружности, вписанной в треугольник ABC
. Пусть d
— радиус этой окружности. Тогда
d=\frac{2S_{\triangle ABC}}{AB+AC+BC}=\frac{2\cdot480}{34+34+60}=\frac{15}{2}.
Треугольники O_{1}OO_{2}
и BOC
подобны, поэтому их высоты OP
и OH
пропорциональны сторонам O_{1}O_{2}
и BC
, т. е. \frac{d-r}{d}=\frac{2r}{BC}
, или \frac{\frac{15}{2}-r}{\frac{15}{2}}=\frac{2r}{60}
. Отсюда находим, что r=6
.
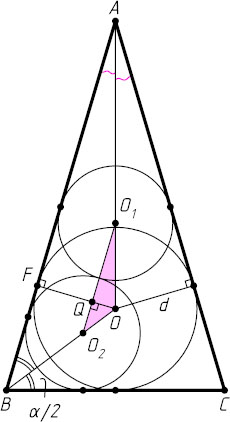
Пусть теперь окружность радиуса r
с центром O_{1}
вписана в угол BAC
, а вторая окружность того же радиуса r
с центром O_{2}
вписана в угол ABC
и касается первой окружности (рис. 4).
Треугольники O_{1}OO_{2}
и AOB
подобны, поэтому их высоты OQ
и OF
пропорциональны сторонам O_{1}O_{2}
и AB
, т. е. \frac{d-r}{d}=\frac{2r}{BC}
, или \frac{\frac{15}{2}-r}{\frac{15}{2}}=\frac{2r}{34}
. Отсюда находим, что r=\frac{255}{49}
.
Источник: ЕГЭ. — 2012 г., задача C4, вариант 11



