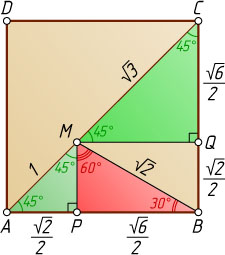
5397. На диагонали AC
квадрата ABCD
взята точка M
. Расстояния от точки M
до вершин A
и B
равны 1 и \sqrt{2}
соответственно. Найдите угол AMB
и расстояние от точки M
до вершины C
.
Ответ. 105^{\circ}
, \sqrt{3}
.
Решение. Пусть P
— проекция точки M
на сторону AB
. Из равнобедренного прямоугольного треугольника APM
находим, что
\angle AMP=45^{\circ},~PM=\frac{\sqrt{2}}{2}.
В прямоугольном треугольнике BMP
катет PM=\frac{\sqrt{2}}{2}
равен половине гипотенузы MB=\sqrt{2}
, значит, \angle MBP=30^{\circ}
, \angle BMP=60^{\circ}
. Следовательно,
\angle AMB=\angle AMP+\angle BMP=45^{\circ}+60^{\circ}=105^{\circ}.
Пусть Q
— проекция точки M
на сторону BC
. Из прямоугольного треугольника BMP
и равнобедренного прямоугольного треугольника CQM
находим, что
BP=PM\tg60^{\circ}=\frac{\sqrt{2}}{2}\cdot\sqrt{3}=\frac{\sqrt{6}}{2},
CM=QM\sqrt{2}=BP\sqrt{2}=\frac{\sqrt{6}}{2}\cdot\sqrt{2}=\sqrt{3}.
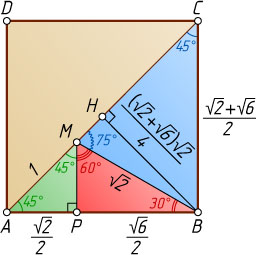
Примечание. С помощью полученных результатов можно вычислить \cos15^{\circ}
и \sin15^{\circ}
. Для этого рассмотрим треугольник BMC
, в котором
\angle BMC=180^{\circ}-105^{\circ}=75^{\circ},~MB=\sqrt{2},~MC=\sqrt{3},~BC=BQ+QC=\frac{\sqrt{2}+\sqrt{6}}{2}.
Пусть BH
— высота треугольника BMC
. Тогда
BH=BC\sin45^{\circ}=\frac{\sqrt{2}+\sqrt{6}}{2}\cdot\frac{\sqrt{2}}{2}=\frac{(\sqrt{2}+\sqrt{6})\sqrt{2}}{4}.
Следовательно,
\cos15^{\circ}=\sin75^{\circ}=\frac{BH}{MB}=\frac{(\sqrt{2}+\sqrt{6})\sqrt{2}}{4\sqrt{2}}=\frac{\sqrt{6}+\sqrt{2}}{4},
\sin15^{\circ}=\sqrt{1-\cos^{2}15^{\circ}}=\frac{\sqrt{6}-\sqrt{2}}{4}.
Источник: Готман Э. Г., Скопец З. А. Решение геометрических задач аналитическим методом: Пособие для учащихся 9—10 кл. — М.: Просвещение, 1979. — № 238, с. 38

