5401. Три одинаковых треугольника разрезаны по разным медианам. Сложите из шести полученных кусков один треугольник.

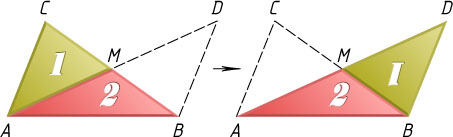
Решение. Пусть AM
— медиана треугольника ABC
. На продолжении отрезка AM
за точку M
отложим отрезок MD
, равный AM
. Тогда треугольник BMD
равен треугольнику CMA
, а треугольник ABD
составлен из треугольников, на которые медиана AM
разбивает треугольник ABC
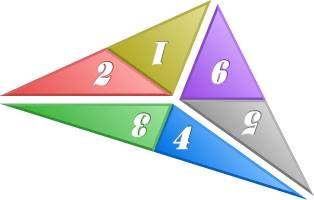
. Аналогично для двух других медиан. Из трёх полученных таким образом треугольников, располагая их так, как показано на рисунке, составим треугольник.

Источник: Произволов В. В. Задачи на вырост. — М.: МИРОС, 1995. — № 4, с. 13
Источник: Турнир им. М. В. Ломоносова. — 2001, 10-11 класс



