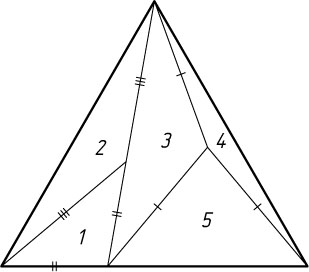
5407. Равносторонний треугольник разрезан на пять равнобедренных треугольников с попарно различными углами при вершинах так, как показано на рисунке. Найдите углы при основаниях этих равнобедренных треугольников.
Ответ. 40^{\circ}
, 20^{\circ}
, 30^{\circ}
, 10^{\circ}
, 50^{\circ}
.
Решение. Пусть углы при основании треугольника n
равны \alpha_{n}
. Тогда
2\alpha_{2}=\alpha_{1},~\alpha_{1}+\alpha_{2}=60^\circ,
откуда
\alpha_{1}=40^{\circ},~\alpha_{2}=20^{\circ};
\alpha_{3}+\alpha_{4}=60^{\circ}-\alpha_{2}=40^{\circ},~\alpha_{4}+\alpha_{5}=60^{\circ},~\alpha_{5}+\alpha_{3}=2\alpha_{1}=80^{\circ},
следовательно,
\alpha_{3}=30^{\circ},~\alpha_{4}=10^{\circ},~\alpha_{5}=50^{\circ}.


