5410. Две окружности пересекаются прямой l
(см. рисунок). Докажите, что угол ABC
равен углу DEM
.
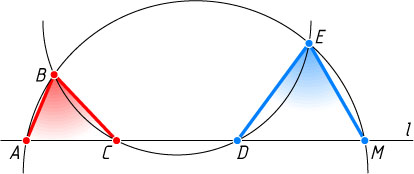
Указание. Примените свойство вписанного четырёхугольника (см. задачу 6).
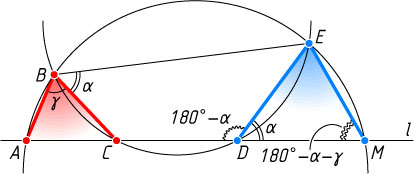
Решение. Обозначим \angle ABC=\gamma
, \angle CBE=\alpha
. Четырёхугольник BEDC
вписанный, поэтому
\angle MDE=180^{\circ}-\angle CDE=180^{\circ}-(180^{\circ}-\angle CBE)=\angle CBE=\alpha.
Четырёхугольник ABEM
также вписанный, поэтому
\angle AME=180^{\circ}-\angle ABE=180^{\circ}-\alpha-\gamma.
Следовательно,
\angle DEM=180^{\circ}-\angle MDE-\angle AME=
=180^{\circ}-\alpha-(180^{\circ}-\alpha-\gamma)=\gamma=\angle ABC.
Что и требовалось доказать.
Источник: Турнир им. М. В. Ломоносова. — 1983
Источник: Бугаенко В. О. Турниры им. Ломоносова. Конкурсы по математике. — 2-е изд. — М.: ТЕИС, 1995. — № 7, с. 11

