5429. Есть три треугольника: остроугольный, прямоугольный и тупоугольный. Саша взял себе один треугольник, а Боря — два оставшихся. Оказалось, что Боря может приложить (без наложения) один из своих треугольников к другому, и получить треугольник, равный Сашиному. Какой из этих треугольников взял Саша?
Ответ. Прямоугольный.
Решение. Заметим, что Саша может разрезать одной прямой свой треугольник на два, равных Бориным. При этом один из концов отрезка расположен в вершине исходного треугольника, а другой — на противоположной стороне.
Допустим, что Саша взял остроугольный треугольник. Посмотрим на сторону, которую пересёк разрез. Если разрез перпендикулярен этой стороне, получится два прямоугольных треугольника. Иначе получится один остроугольный и один тупоугольный треугольник. Ни один из этих вариантов не соответствует условию задачи, поэтому Саша не мог взять остроугольный треугольник.
Допустим теперь, что Саша взял тупоугольный треугольник. Посмотрим опять на сторону, которую пересёк разрез. Если разрез перпендикулярен этой стороне, получится два прямоугольных треугольника. Иначе один из получившихся треугольников — тупоугольный. В любом случае условие задачи не выполнено, а значит, этот случай невозможен.
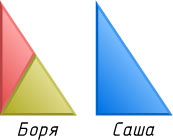
Поэтому Саша взял прямоугольный треугольник. Соответствующий пример приведён на рисунке.

Источник: Турнир им. М. В. Ломоносова. — 2006, 6-9 класс