5430. На рисунке изображена фигура ABCD
. Стороны AB
, CD
и AD
этой фигуры — отрезки (причём AB\parallel CD
и AD\perp CD
); BC
— дуга окружности, причём любая касательная к этой дуге отсекает от фигуры трапецию или прямоугольник. Объясните, как провести касательную к дуге BC
, чтобы отсекаемая фигура имела наибольшую площадь.
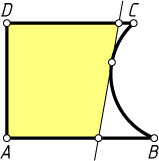
Ответ. Касательную к дуге BC
надо провести через точку пересечения этой дуги с серединным перпендикуляром к отрезку AD
.
Решение. Воспользуемся формулой площади трапеции — площадь равна произведению средней линии на высоту.
В нашем случае боковыми сторонами трапеции будут отрезок AD
и касательная MN
, а основаниями трапеции (или прямоугольника) — отрезки AM
и DN
. Высота трапеции (расстояние между основаниями, равное, например, перпендикулярному основаниям отрезку AD
) не зависит от выбора положения касательной. А вот среднюю линию можно менять.
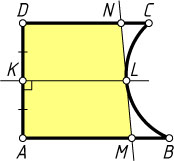
Проведём серединный перпендикуляр к отрезку AD
. Обозначим точки его пересечения с AD
и с дугой BC
через K
и L
соответственно. Заметим, что средняя линия получаемых трапеций всегда будет лежать на отрезке KL
. Значит, площадь максимальна, если средняя линия совпадает с отрезком KL
. Поэтому следует провести касательную через точку L
.
Источник: Турнир им. М. В. Ломоносова. — 2007, 9-11 класс

