5432. Прямоугольник площади 14 делит сторону квадрата в отношении 1:3
(см. рис.). Найдите площадь квадрата.
Ответ. 50.
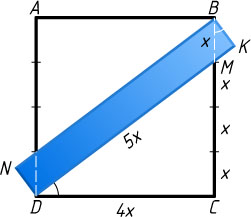
Решение. Первый способ. Пусть ABCD
— квадрат со стороной 4x
, BKDN
— прямоугольник площади 14, причём стороны BC
и DK
пересекаются в точке M
, BM=x
и CM=3x
(рис. 1).
Из прямоугольного треугольника CDM
находим, что
DM=\sqrt{CM^{2}+CD^{2}}=\sqrt{(3x)^{2}+(4x)^{2}}=5x,
Прямоугольный треугольник KBM
подобен треугольнику CDM
по двум углам, причём коэффициент подобия равен отношению их гипотенуз, т. е. \frac{1}{5}
. Значит, катеты меньшего треугольника равны MK=\frac{3}{5}x
и BK=\frac{4}{5}x
. Поэтому площадь прямоугольника равна
DK\cdot BK=(DM+MK)\cdot BK=\left(5+\frac{3}{5}\right)x\cdot\frac{4}{5}x=\frac{28\cdot4}{25}x^{2}=14\cdot\frac{8}{25}x^{2}.
С другой стороны, по условию задачи она равна 14. Значит, x^{2}=\frac{25}{8}
, а искомая площадь квадрата равна
BC^{2}=(4x)^{2}=16x^{2}=16\cdot\frac{25}{8}=50.
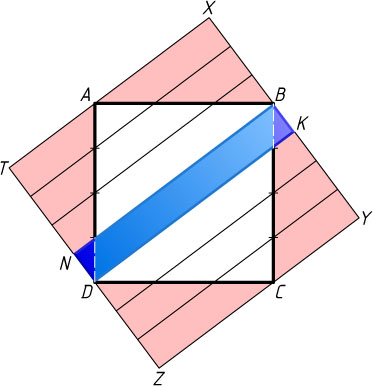
Второй способ. Через вершины A
и C
квадрата ABCD
проведём прямые, параллельные большей стороне BK
прямоугольника BKDN
. Пусть эти прямые пересекаются с прямыми BK
и DN
точках X
, Y
, Z
и T
(рис. 2). Получим квадрат XYZT
, состоящий из исходного квадрата ABCD
и четырёх равных прямоугольных треугольников.
Разделим сторону BC
квадрата ABCD
на четыре равные части и через точки деления проведём прямые, параллельные DK
. Получим четыре прямоугольника, равных прямоугольнику BKDN
. Аналогично поступим со стороной AD
. В результате окажется, что квадрат XYZT
состоит из семи прямоугольников, площадь каждого из которых равна площади прямоугольника BKND
, т. е. 14. Значит, площадь квадрата XYZT
равна 14\cdot7=98
, а его сторона равна \sqrt{98}=7\sqrt{2}
. Тогда
BK=\frac{1}{7}XY=\sqrt{2},~BY=4BK=4\sqrt{2},~CY=BX=3BK=3\sqrt{2}.
Поэтому площадь каждого из четырёх прямоугольных треугольников, дополняющих исходный квадрат до квадрата XYZT
, равна \frac{1}{2}\cdot4\sqrt{2}\cdot3\sqrt{2}=12
. Следовательно, площадь квадрата ABCD
равна
98-4\cdot12=98-48=50.
