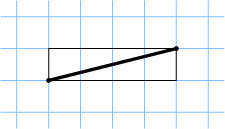
5433. На клетчатой бумаге проведена диагональ прямоугольника 1\times4
. Покажите, как, пользуясь только линейкой без делений, разделить этот отрезок на три равные части.
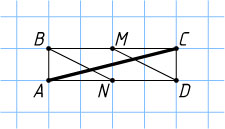
Решение. Пусть ABCD
— прямоугольник со сторонами AB=CD=1
, BC=AD=4
; точки M
и N
лежат на сторонах BC
и AD
соответственно, причём BM=MC=DN=AN=2
. Противоположные стороны BM
и DN
четырёхугольника BMDN
равны и параллельны, значит, это параллелограмм. Тогда BN\parallel DM
. По теореме Фалеса прямые BN
и DM
делят диагональ AC
на три равные части.
Источник: Турнир им. М. В. Ломоносова. — 2010, 9-11 класс

