5523. Окружности радиусов 5 и 8 с центрами соответственно O_{1}
и O_{2}
касаются в точке A
. Прямая, проходящая через точку A
, вторично пересекает меньшую окружность в точке B
, а большую — в точке C
. Найдите площадь треугольника BCO_{2}
, если \angle ABO_{1}=15^{\circ}
.
Ответ. 6 или 26.
Решение. Возможны два случая.
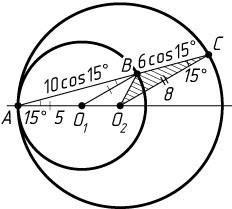
Первый случай. Окружности касаются внутренним образом (рис. 1). Точки O_{2}
, O_{1}
и A
лежат на одной прямой. Треугольники BO_{1}A
и CO_{2}A
равнобедренные, значит, \angle ACO_{2}=\angle BAO_{1}=\angle ABO_{1}=15^{\circ}
. Отсюда получаем, что AB=2AO_{1}\cos15^{\circ}=10\cos15^{\circ}
.
Аналогично находим, что AC=16\cos15^{\circ}
, а так как окружности касаются внутренним образом, то BC=AC-AB=16\cos15^{\circ}-10\cos15^{\circ}=6\cos15^{\circ}
. Следовательно,
S_{\triangle BCO_{2}}=\frac{1}{2}O_{2}C\cdot BC\sin\angle BCO_{2}=\frac{1}{2}\cdot8\cdot6\cos15^{\circ}\sin15^{\circ}=
=12\cdot2\cos15^{\circ}\cdot\sin15^{\circ}=12\sin30^{\circ}=6.
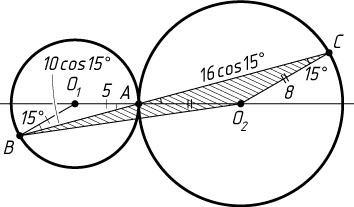
Второй случай. Окружности касаются внешним образом (рис. 2). Как и в первом случае
\angle BCO_{2}=\angle CAO_{2}=\angle BAO_{1}=\angle ABO_{1}=15^{\circ},~AB=10\cos15^{\circ},~AC=16\cos15^{\circ}.
Окружности касаются внешним образом, поэтому BC=AB+AC=10\cos15^{\circ}+16\cos15^{\circ}=26\cos15^{\circ}
. Следовательно,
S_{\triangle BCO_{2}}=\frac{1}{2}O_{2}C\cdot BC\sin\angle BCO_{2}=\frac{1}{2}\cdot8\cdot26\cos15^{\circ}\sin15^{\circ}=
=52\cdot2\cos15^{\circ}\cdot\sin15^{\circ}=52\sin30^{\circ}=26.
Источник: ЕГЭ. — 2013
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.51, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 9.51.1, с. 95

