5566. Окружность радиуса 6\sqrt{2}
вписана в прямой угол. Вторая окружность также вписана в этот угол и пересекается с первой в точках M
и N
. Известно, что расстояние между центрами окружностей равно 8. Найдите MN
.
Ответ. 4\sqrt{14}
или 4\sqrt{2}
.
Решение. Пусть O_{1}
— центр окружности радиуса 6\sqrt{2}
, O_{2}
— центр второй окружности, A
— вершина данного прямого угла. Поскольку окружности вписаны в угол, их центры O_{1}
и O_{2}
лежат на его биссектрисе, поэтому AO_{1}=\frac{6\sqrt{2}}{\cos45^{\circ}}=12
. Возможны два случая.
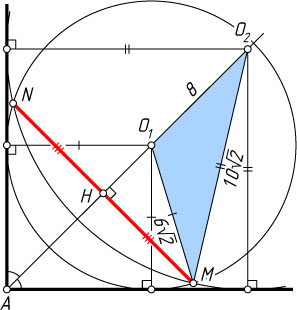
Первый случай. Точка O_{1}
лежит между A
и O_{2}
. Тогда AO_{2}=AO_{1}+O_{1}O_{2}=12+8=20
, а радиус второй окружности равен AO_{2}\cos45^{\circ}=10\sqrt{2}
.
В треугольнике O_{1}MO_{2}
известно, что O_{1}O_{2}=8
, O_{1}M=6\sqrt{2}
, O_{2}M=10\sqrt{2}
. Общая хорда MN
окружностей перпендикулярна линии центров O_{1}O_{2}
и делится ею пополам, поэтому высота MH
треугольника O_{1}MO_{2}
равна половине MN
.
Пусть p
— полупериметр треугольника O_{1}MO_{2}
. Тогда
p=\frac{O_{1}O_{2}+O_{1}M+O_{2}M}{2}=\frac{8+6\sqrt{2}+10\sqrt{2}}{2}=4+8\sqrt{2}.
По формуле Герона
S_{\triangle O_{1}MO_{2}}=\sqrt{p(p-O_{1}O_{2})(p-O_{1}M)(p-O_{2}M)}=
=\sqrt{(4+8\sqrt{2})(8\sqrt{2}-4)(4+2\sqrt{2})(4-2\sqrt{2})}=
=\sqrt{(128-16)(16-8)}=\sqrt{112\cdot8}=8\sqrt{14}.
С другой стороны,
S_{\triangle O_{1}MO_{2}}=\frac{1}{2}O_{1}O_{2}\cdot MH=\frac{1}{2}\cdot8\cdot MH=4MH.
Из равенства 4MH=8\sqrt{14}
находим, что MH=2\sqrt{14}
. Следовательно, MN=2MH=4\sqrt{14}
.
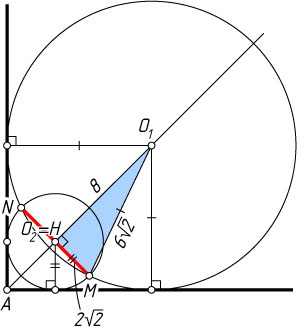
Второй случай. Точка O_{2}
лежит между A
и O_{1}
. Тогда AO_{2}=AO_{1}-O_{1}O_{2}=12-8=4
, а радиус второй окружности равен AO_{2}\cos45^{\circ}=2\sqrt{2}
.
В треугольнике O_{1}MO_{2}
известно, что O_{1}O_{2}=8
, O_{1}M=6\sqrt{2}
, O_{2}M=2\sqrt{2}
. Аналогично первому случаю находим, что
p=\frac{8+6\sqrt{2}+2\sqrt{2}}{2}=4+4\sqrt{2},
S_{\triangle O_{1}MO_{2}}=\sqrt{(4+4\sqrt{2})(4\sqrt{2}-4)(4-2\sqrt{2})(4+2\sqrt{2})}=
=\sqrt{(32-16)(16-8)}=\sqrt{16\cdot8}=8\sqrt{2}.
С другой стороны,
S_{\triangle O_{1}MO_{2}}=\frac{1}{2}O_{1}O_{2}\cdot MH=\frac{1}{2}\cdot8\cdot MH=4MH.
Из равенства 4MH=8\sqrt{2}
находим, что MH=2\sqrt{2}
. Следовательно, MN=2MH=4\sqrt{2}
.
Примечание. Высоту MH
треугольника O_{1}MO_{2}
можно найти, применив к нему теорему косинусов.
Источник: ЕГЭ. — 2013

