5606. На стороне AB
и диагонали AC
квадрата ABCD
отмечены точки M
и N
соответственно, причём AM:MB=1:4
и AN:NC=3:2
.
а) Докажите, что точки A
, M
, N
и D
лежат на одной окружности.
б) Найдите расстояние от точки пересечения диагоналей четырёхугольника AMND
до прямой MN
, если сторона квадрата равна 30.
Ответ. \sqrt{13}
.
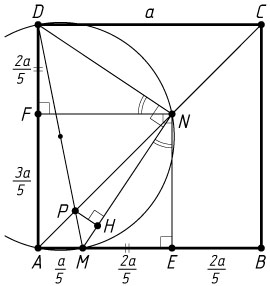
Решение. а) Пусть E
и F
— проекции точки N
на стороны AB
и AD
соответственно. Тогда
\frac{AE}{AB}=\frac{AN}{AC}=\frac{3}{5},~\frac{DF}{AD}=\frac{CN}{AC}=\frac{2}{5},
ME=AE-AM=\frac{3}{5}AB-\frac{1}{5}AB=\frac{2}{5}AB,
DF=\frac{2}{5}AD=\frac{2}{5}AB=ME.
Кроме того NE=NF
, так как точка N
лежит на диагонали квадрата. Прямоугольные треугольники MEN
и DFN
равны по двум катетам, значит, \angle MNE=\angle DNF
, а так как \angle ENF=90^{\circ}
, то
\angle MND=\angle MNF+\angle DNF=\angle MNF+\angle MNE=90^{\circ}.
Из точек A
и N
отрезок DM
виден под прямым углом, следовательно, эти точки лежат на окружности с диаметром DM
.
б) Обозначим через a
сторону квадрата. Пусть P
— точка пересечения диагоналей четырёхугольника AMND
. Треугольник APM
подобен треугольнику CPD
с коэффициентом \frac{AM}{CD}=\frac{\frac{1}{5}a}{a}=\frac{1}{5}
, значит, \frac{MP}{PD}=\frac{1}{5}
, поэтому \frac{MP}{MD}=\frac{1}{6}
.
Пусть H
— основание перпендикуляра, опущенного из точки P
на MN
. Тогда PH\parallel DN
, так как DN\perp MN
. Треугольник MPH
подобен треугольнику MDN
, причём коэффициент подобия равен \frac{MP}{MD}=\frac{1}{6}
. Следовательно,
PH=\frac{1}{6}DN=\frac{1}{6}\sqrt{DF^{2}+NF^{2}}=\frac{1}{6}\sqrt{\left(\frac{2}{5}a\right)^{2}+\left(\frac{3}{5}a\right)^{2}}=
=\frac{1}{6}\cdot\frac{a\sqrt{13}}{5}=\frac{a\sqrt{13}}{30}=\frac{30\sqrt{13}}{30}=\sqrt{13}.
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.44.1, с. 152; № 5, с. 176
