5704. Дан параллелограмм ABCD
и точка M
. Через точки A
, B
, C
и D
проведены прямые, параллельные прямым MC
, MD
, MA
и MB
соответственно. Докажите, что проведённые прямые пересекаются в одной точке.
Указание. Рассмотрите образ точки M
при симметрии относительно точки пересечения диагоналей параллелограмма ABCD
.
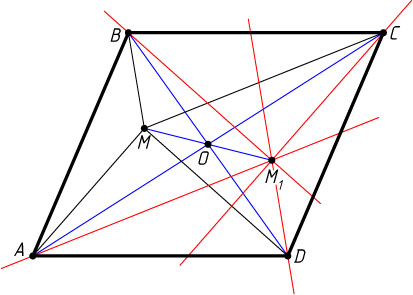
Решение. Пусть M_{1}
— образ точки M
при симметрии относительно точки O
пересечения диагоналей параллелограмма ABCD
. При этой симметрии вершина A
переходит в вершину C
. Следовательно, прямая M_{1}C
параллельна прямой MA
. Аналогично докажем, что прямые M_{1}A
, M_{1}B
и M_{1}D
соответственно параллельны MC
, MD
и MB
. Поскольку через данную точку, не лежащую на прямой, проходит единственная прямая, параллельная этой прямой, то утверждение доказано.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 4, с. 47
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4, с. 353
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.09, с. 162
