5713. Окружности с центрами O_{1}
и O_{2}
касаются внешним образом; прямая касается окружностей в различных точках A
и B
соответственно. Известно, что точка пересечения диагоналей четырёхугольника O_{1}ABO_{2}
лежит на меньшей из окружностей. Найдите отношение радиусов окружностей.
Ответ. 1:2
.
Указание. Треугольник BO_{1}O_{2}
— равнобедренный.
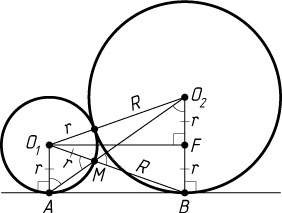
Решение. Пусть O_{1}
— центр меньшей окружности. Прямые O_{1}A
и O_{2}B
параллельны, так как они перпендикулярны одной и той же прямой AB
, поэтому \angle BO_{2}M=\angle MAO_{1}
. Треугольник MBO_{2}
подобен равнобедренному треугольнику MAO_{1}
по двум углам. Следовательно, треугольник MBO_{2}
также равнобедренный.
Обозначим O_{1}A=r
, O_{2}B=R
. Тогда O_{1}M=O_{1}A=r
и MB=O_{2}B=R
, поэтому O_{1}B=O_{1}M+MB=r+R
, а так как линия центров касающихся окружностей проходит через точку их касания, O_{1}O_{2}=r+R
. Значит, треугольник BO_{1}O_{2}
равнобедренный. Его высота O_{1}F
является медианой, а так как O_{1}ABF
прямоугольник, то FB=O_{1}A=r
. Значит, 2r=R
. Следовательно, \frac{r}{R}=\frac{1}{2}
.
Автор: Гордин Р. К.
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 9.53, с. 88
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 9.53.1, с. 96
