5722. С центром в вершине D
квадрата ABCD
построена окружность, проходящая через вершины A
и C
. Через середину M
стороны AB
проведена касательная к этой окружности, пересекающая сторону BC
в точке K
. Найдите отношение BK:KC
.
Ответ. 2.
Указание. Примените теорему Пифагора к треугольнику MBK
.
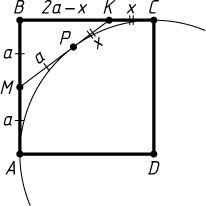
Решение. Пусть P
— точка касания окружности с отрезком MK
. Обозначим AM=MB=a
, KC=x
. Тогда
MP=MA=a,~KP=KC=x,~BK=BC-KC=2a-x,~MK=MP+PK=a+x.
По теореме Пифагора MK^{2}=MB^{2}+BK^{2}
, или (a+x)^{2}=a^{2}+(2a-x)^{2}
, откуда x=\frac{2}{3}a
. Поэтому
KC=\frac{2}{3}a,~BK=2a-\frac{2}{3}a=\frac{4}{3}a,~\frac{BK}{KC}=\frac{\frac{4}{3}a}{\frac{2}{3}a}=2.
Автор: Гордин Р. К.
