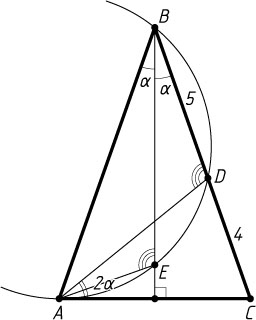
5767. В равнобедренном треугольнике ABC
с основанием AC
вершины A
, B
и точка пересечения высот треугольника E
лежат на окружности, которая пересекает отрезок BC
в точке D
. Найдите радиус окружности, если CD=4
, BD=5
.
Ответ. \frac{27\sqrt{2}}{8}
.
Решение. Пусть AK
и BM
— высоты треугольника ABC
. Тогда BM
— медиана и биссектриса равнобедренного треугольника ABC
. Обозначим \angle MBC=\alpha
. Тогда
\angle BCA=\angle CAB=90^{\circ}-\alpha,~\angle AEB=\angle MEK=180^{\circ}-(90^{\circ}-\alpha)=90^{\circ}+\alpha.
Вписанные в данную окружность углы ADB
и AEB
опираются на одну и ту же дугу, поэтому
\angle ADB=\angle AEB=90^{\circ}+\alpha.
По теореме о внешнем угле треугольника
\angle CAD=\angle ADB-\angle ACD=(90^{\circ}+\alpha)-(90^{\circ}-\alpha)=2\alpha,
поэтому
\angle BAD=\angle BAC-\angle CAD=(90^{\circ}-\alpha)-2\alpha=90^{\circ}-3\alpha.
Известно, что BD=5
и AB=BC=BD+DC=5+4=9
. Применяя теорему синусов к треугольнику ABD
, получим, что \frac{AB}{\sin(90^{\circ}+\alpha)}=\frac{BD}{\sin(90^{\circ}-3\alpha)}
, или \frac{9}{\cos\alpha}=\frac{5}{\cos3\alpha}
, а так как \cos3\alpha=\cos\alpha(4\cos^{2}\alpha-3)
, то после очевидных упрощений найдём, что \cos\alpha=\frac{2\sqrt{2}}{3}
.
Если R
— искомый радиус, то
R=\frac{AB}{2\sin(90^{\circ}+\alpha)}=\frac{9}{9\cos\alpha}=\frac{9}{2\cdot\frac{2\sqrt{2}}{3}}=\frac{27\sqrt{2}}{8}.
Источник: Вступительный экзамен на экономический факультет МГУ. — 2000, билет 1, № 4
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 00-1-4, с. 388
