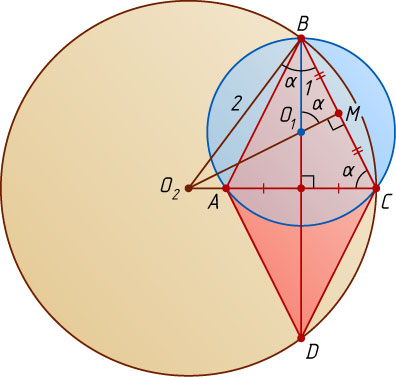
5786. Дан ромб ABCD
. Радиусы окружностей, описанных около треугольников ABC
и BCD
, равны 1 и 2. Найдите расстояние между центрами этих окружностей.
Ответ. \frac{3\sqrt{5}}{5}
.
Решение. Отрезок BC
— общая хорда окружностей с центрами O_{1}
и O_{2}
, описанных около треугольников ABC
и BCD
соответственно, поэтому прямая O_{1}O_{2}
перпендикулярна отрезку BC
и делит его пополам.
Пусть M
— середина BC
. Тогда O_{1}M
и BD
— серединные перпендикуляры к сторонам BC
и AC
треугольника ABC
. Обозначим \angle CBO_{2}=\angle BCO_{2}=\angle BO_{1}M=\alpha
. Из прямоугольных треугольников BMO_{1}
и BMO_{2}
находим, что
BM=BO_{1}\sin\alpha=1\cdot\sin\alpha=\sin\alpha,~BM=O_{2}B\cos\alpha=2\cos\alpha,
откуда \tg\alpha=2
. Тогда \cos\alpha=\frac{1}{\sqrt{5}}
, \sin\alpha=\frac{2}{\sqrt{5}}
, значит,
O_{1}M=BO_{1}\cos\alpha=\frac{1}{\sqrt{5}},~O_{2}M=BO_{2}\sin\alpha=\frac{4}{\sqrt{5}}.
Следовательно,
O_{1}O_{2}=O_{2}M-O_{1}M=\frac{4}{\sqrt{5}}-\frac{1}{\sqrt{5}}=\frac{3}{\sqrt{5}}.
Источник: Вступительный экзамен в МФТИ. — 1998, билет 8, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 98-8-3, с. 380
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 10.8, с. 76
