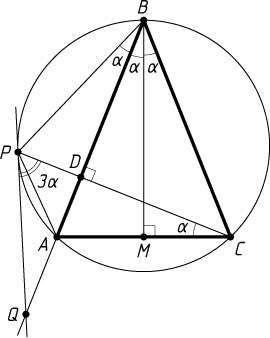
5787. Равнобедренный треугольник ABC
(AB=BC
) вписан в окружность. Прямая CD
, перпендикулярная AB
, пересекает окружность в точке P
. Касательная к окружности, проходящая через точку P
, пересекает прямую AB
в точке Q
. Найдите отрезки PA
и PQ
, если AC=5
, \angle ABC=2\arccos\sqrt{\frac{5}{6}}
.
Ответ. \sqrt{\frac{15}{2}}
, 6.
Решение. Будем считать, что точка D
лежит на прямой AB
. Пусть BM
— высота и медиана треугольника ABC
. Обозначим \angle ABM=\alpha
. Тогда
\cos\alpha=\sqrt{\frac{5}{6}},~\sin\alpha=\sqrt{\frac{1}{6}},
\sin2\alpha=2\sin\alpha\cos\alpha=2\sqrt{\frac{5}{6}}\cdot\sqrt{\frac{1}{6}}=\frac{\sqrt{5}}{3},~\cos2\alpha=\sqrt{1-\frac{5}{9}}=\frac{2}{3},
\sin3\alpha=\sin(\alpha+2\alpha)=\sin\alpha\cos2\alpha+\cos\alpha\sin2\alpha=\sqrt{\frac{1}{6}}\cdot\frac{2}{3}+\sqrt{\frac{5}{6}}\cdot\frac{\sqrt{5}}{3}=\frac{7\sqrt{6}}{18}.
\cos3\alpha=\sqrt{1-\frac{6\cdot49}{324}}=\frac{\sqrt{30}}{18}.
Если R
— радиус описанной окружности треугольника ABC
, то
R=\frac{AC}{2\sin\angle ABC}=\frac{AC}{2\sin2\alpha}=\frac{5}{2\cdot\frac{\sqrt{5}}{3}}=\frac{3\sqrt{5}}{2}.
Вписанные углы ABP
и ACP
опираются на одну и ту же дугу, поэтому
\angle ABP=\angle ACP=\angle ABM=\alpha,
значит,
\angle PBC=\angle ABP+\angle ABC=\alpha+2\alpha=3\alpha.
Из теоремы об угле между касательной и хордой
\angle CPQ=\angle PBC=3\alpha.
Следовательно,
PA=2R\sin\angle ABP=2R\sin\alpha=3\sqrt{5}\cdot\frac{1}{\sqrt{6}}=\sqrt{\frac{15}{2}},
CP=2R\sin\angle PBC=3\sqrt{5}\cdot\frac{7\sqrt{6}}{18}=\frac{7\sqrt{30}}{6},
CD=AC\cos\angle ACD=AC\cos\alpha=5\cdot\sqrt{\frac{5}{6}}=\frac{5\sqrt{30}}{6},
PD=CP-CD=\frac{7\sqrt{30}}{6}-\frac{5\sqrt{30}}{6}=\frac{\sqrt{30}}{3}.
Наконец, из прямоугольного треугольника PDQ
находим, что
PQ=\frac{PD}{\cos\angle CPQ}=\frac{PD}{\cos3\alpha}=\frac{\frac{\sqrt{30}}{3}}{\frac{\sqrt{30}}{18}}=6.
Источник: Вступительный экзамен в МФТИ. — 1996, билет 1, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 96-1-3, с. 356
