5836. Медиана AM
и биссектриса CD
прямоугольного треугольника ABC
(\angle B=90^{\circ}
) пересекаются в точке O
. Найдите площадь треугольника ABC
, если CO=9
, OD=5
.
Ответ. \frac{1323}{20}
.
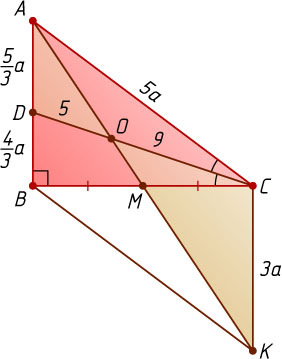
Решение. На продолжении медианы AM
за точку M
отложим отрезок MK
, равный AM
. Тогда четырёхугольник ABKC
параллелограмм, так как его диагонали BC
и AK
делятся точкой пересечения M
пополам. Положим AB=3a
. Треугольник AOD
подобен треугольнику KOC
(по двум углам), значит,
AD=KC\cdot\frac{OD}{OC}=AB\cdot\frac{OD}{OC}=AB\cdot\frac{5}{9}=3a\cdot\frac{5}{9}=\frac{5}{3}a,
BD=AB-AD=3a-\frac{5}{3}a=\frac{4}{3}a.
По свойству биссектрисы треугольника
\frac{BC}{AC}=\frac{BD}{AD}=\frac{\frac{4}{3}a}{\frac{5}{3}a}=\frac{4}{5},
а так как AB=3a
, то AC=5a
и BC=4a
. По теореме Пифагора
BC^{2}+BD^{2}=CD^{2},~16a^{2}+\left(\frac{4}{3}a\right)^{2}=14^{2},
откуда находим, что a^{2}=\frac{49\cdot9}{4\cdot10}
Следовательно,
S_{\triangle ABC}=\frac{1}{2}BC\cdot AB=\frac{1}{2}\cdot4a\cdot3a=6a^{2}=6\cdot\frac{49\cdot9}{4\cdot10}=\frac{1323}{20}.
Источник: Вступительный экзамен в МФТИ. — 1994, билет 6, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 94-6-3, с. 341
Источник: Гордин Р. К. ЕГЭ 2010. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2010. — № 2.15, с. 18
