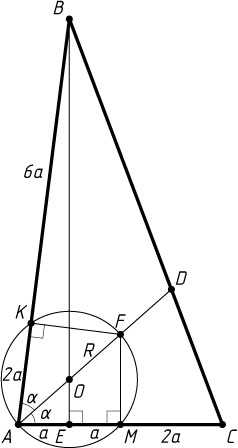
5844. Биссектриса AD
и высота BE
остроугольного треугольника ABC
пересекаются в точке O
. Окружность радиуса R
с центром в точке O
проходит через вершину A
, середину стороны AC
и пересекает сторону AB
в точке K
такой, что AK:KB=1:3
. Найдите длину стороны BC
.
Ответ. \frac{9R}{\sqrt{2}}
.
Решение. Пусть M
— середина стороны AC
, F
— пересечение продолжения радиуса AO
с окружностью. Тогда AF
— диаметр окружности.
Поскольку E
— основание перпендикуляра, опущенного из точки O
на хорду AM
, точка E
— середина AM
. Обозначим AE=a
. Тогда
EM=AE=a,~AM=2a,~AC=2AM=4a.
Точки K
и M
лежат на окружности с диаметром AF
, поэтому \angle AKF=\angle AMF=90^{\circ}
. Из равенства прямоугольных треугольников AKF
и AMF
(по гипотенузе и острому углу) следует, что AK=AM=2a
. Тогда BK=3AK=6a
, AB=8a
.
Обозначим \angle BAD=\angle CAD=\alpha
. Из прямоугольного треугольника ABE
находим, что
\cos2\alpha=\cos\angle BAE=\frac{AE}{AB}=\frac{a}{8a}=\frac{1}{8}.
Тогда
\cos\alpha=\sqrt{\frac{1+\cos2\alpha}{2}}=\sqrt{\frac{1+\frac{1}{8}}{2}}=\frac{3}{4}.
Из прямоугольного треугольника AEO
находим, что a=AE=AO\cos\alpha=\frac{3R}{4}
. По теореме косинусов
BC=\sqrt{AB^{2}+AC^{2}-2AB\cdot AC\cos2\alpha}=\sqrt{64a^{2}+16a^{2}-2\cdot8a\cdot4a\cdot\frac{1}{8}}=
=6a\sqrt{2}=6\sqrt{2}\cdot\frac{3R}{4}=\frac{9R}{\sqrt{2}}.
Источник: Вступительный экзамен в МФТИ. — 1993, билет 2, № 3
Источник: Сборник методических материалов письменных испытаний по математике и физике абитуриентов Московского Физтеха (1947—2006 гг.). Математика / Сост. Д. А. Александров, И. Г. Почернин, И. Г. Проценко, И. Е. Сидорова, В. Б. Трушин, И. Г. Шомполов. Под ред. И. Г. Шомполова. — М.: МФТИ, 2007. — № 93-2-3, с. 329
