5892. Сторона CD
прямоугольника ABCD
касается некоторой окружности в точке M
. Продолжение стороны AD
последовательно пересекает окружность в точках P
и Q
, прямая BC
касается окружности, а точка Q
лежит на прямой BM
.
а) Докажите, что \angle DMP=\angle CBM
.
б) Известно, что CM=5
и CD=8
. Найдите сторону AD
.
Ответ. 15.
Решение. а) Поскольку DMP
— угол между касательной MD
и хордой MP
, а MQP
— угол, вписанный в окружность, то
\angle DMP=\angle MQP=\angle MQD
(каждый из этих угол равен половине меньшей дуги MP
), а так как \angle MQD=\angle CBM
(по свойству параллельных прямых), то \angle DMP=\angle CBM
.
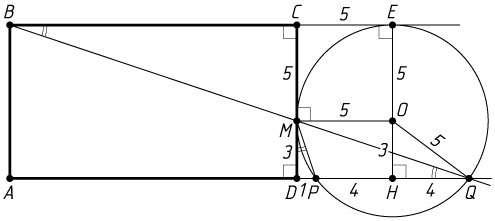
б) Пусть окружность с центром O
касается прямой BC
в точке E
, а H
— основание перпендикуляра, опущенного из точки O
на PQ
. Тогда H
— середина хорды PQ
. Из прямоугольного треугольника OHQ
находим, что
HQ=\sqrt{OQ^{2}-OH^{2}}=\sqrt{OQ^{2}-DM^{2}}=\sqrt{5^{2}-(8-5)^{2}}=\sqrt{25-9}=4.
Поскольку OE\perp PQ
, точки O
, E
и H
лежат на одной прямой и CDHE
— прямоугольник, а так как CE=CM=5
, то
DQ=DH+HQ=CE+HQ=CM+HQ=5+4=9.
Треугольник BCM
подобен треугольнику QDM
с коэффициентом \frac{CM}{DM}=\frac{5}{3}
, следовательно,
AD=BC=\frac{5}{3}DQ=\frac{5}{3}\cdot9=15.
Источник: Диагностические и тренировочные задачи ЕГЭ. — 2014
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 8.37.1, с. 84
