6005. На сторонах BC
и CD
квадрата ABCD
взяты точки M
и K
соответственно, причём \angle BAM=\angle MAK
. Докажите, что BM+KD=AK
.
Указание. Поверните квадрат ABCD
относительно вершины A
на 90^{\circ}
так, чтобы вершина B
перешла в вершину D
.
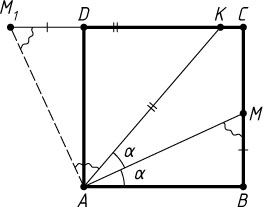
Решение. Повернём квадрат ABCD
относительно вершины A
на 90^{\circ}
так, чтобы вершина B
перешла в вершину D
. Тогда точка M
перейдёт в точку M_{1}
, лежащую на продолжении стороны CD
за точку D
, и M_{1}D=BM
.
Обозначим \angle BAM=\angle MAK=\alpha
. Тогда
\angle MAM_{1}=90^{\circ},~\angle AM_{1}K=\angle AM_{1}D=\angle AMB=90^{\circ}-\alpha,
\angle M_{1}AK=\angle MAM_{1}-\angle MAK=90^{\circ}-\alpha=\angle AM_{1}K.
Значит, треугольник AKM_{1}
— равнобедренный. Следовательно,
AK=KM_{1}=KD+DM_{1}=KD+BM.
Источник: Турнир городов. — 1997-1998, XIX, осенний тур, младшие классы, тренировочный вариант
Источник: Моденов П. С. Сборник задач по специальному курсу элементарной математики. — М.: Советская наука, 1957. — № 3, с. 178
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 18.1, с. 69
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.1, с. 374
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 790, с. 98
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 22.28, с. 206
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 1.110, с. 181
