6033. Пусть P
, Q
и R
— центры равносторонних треугольников, построенных внешним образом на сторонах AB
, BC
и AC
треугольника ABC
, а M
, N
и K
— центры равносторонних треугольников, построенных на сторонах треугольника ABC
внутренним образом. Докажите, что разность площадей треугольников PQR
и MNK
равна площади треугольника ABC
.
Указание. Выразите по теореме косинусов стороны равносторонних треугольников PQR
и MNK
через две стороны и угол между ними треугольника ABC
.
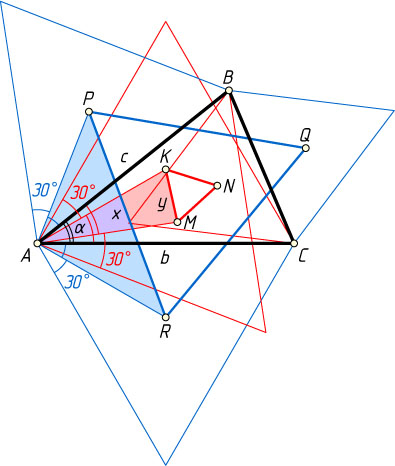
Решение. Пусть x
и y
— стороны равносторонних треугольников PQR
и MNK
, AC=b
, AB=c
, \angle BAC=\alpha
. По теореме косинусов из треугольника APR
находим, что
x^{2}=PR^{2}=AR^{2}+AP^{2}-2AR\cdot AP\cos\angle PAR=
=\left(\frac{b}{\sqrt{3}}\right)^{2}+\left(\frac{c}{\sqrt{3}}\right)^{2}-\frac{2}{3}bc\cos(\alpha+60^{\circ})=
=\frac{1}{3}(b^{2}+c^{2}-2bc\cos(\alpha+60^{\circ})).
Тогда
S_{\triangle PQR}=\frac{x^{2}\sqrt{3}}{4}=\frac{\sqrt{3}}{12}(b^{2}+c^{2}-2bc\cos(\alpha+60^{\circ})).
Аналогично
y^{2}=MK^{2}=\frac{1}{3}(b^{2}+c^{2}-2bc\cos(\alpha-60^{\circ})),
S_{\triangle MNK}=\frac{y^{2}\sqrt{3}}{4}=\frac{\sqrt{3}}{12}(b^{2}+c^{2}-2bc\cos(\alpha-60^{\circ})).
Следовательно,
S_{\triangle PQR}-S_{\triangle MNK}=\frac{\sqrt{3}}{6}bc(\cos(\alpha-60^{\circ})-\cos(\alpha+60^{\circ}))=
=\frac{\sqrt{3}}{3}bc\sin\alpha\sin60^{\circ}=\frac{1}{2}bc\sin\alpha=S_{\triangle ABC}.
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 81
Источник: Избранные задачи из журнала «American Mathematical Monthly» / Пер. с англ. Ю. А. Данилова, под ред. В. М. Алексеева. — М.: Мир, 1977. — № 53, с. 26
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 2. — М.: Наука, 1991. — № 18.38, с. 72
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 18.42(в), с. 377
Источник: Куланин Е. Д., Федин С. Н. Геометрия треугольника в задачах: Экспериментальное учебное пособие для 8—10 кл. школ физико-математического направления. — М.: НИИ школ, 1990. — № 46, с. 10
