6037. Точка P
расположена внутри квадрата ABCD
, причём AP:BP:CP=1:2:3
. Найдите угол APB
.
Ответ. 135^{\circ}
.
Указание. Поверните треугольник APB
на 90^{\circ}
против часовой стрелки вокруг вершины B
.
Решение. Будем считать, что AP=1
, BP=2
, CP=3
. Пусть P_{1}
— образ точки P
при повороте на 90^{\circ}
вокруг вершины B
, переводящем точку A
в C
. Тогда PBP_{1}
— равнобедренный прямоугольный треугольник. Поэтому
\angle BP_{1}P=45^{\circ},~P_{1}P=2\sqrt{2}.
Следовательно,
PP^{2}_{1}+P_{1}C^{2}=8+1=9=3^{2}=PC^{2}.
Значит, треугольник PP_{1}C
— прямоугольный, \angle PP_{1}C=90^{\circ}
. Следовательно,
\angle APB=\angle CP_{1}B=\angle CP_{1}P+\angle BP_{1}P=90^{\circ}+45^{\circ}=135^{\circ}.
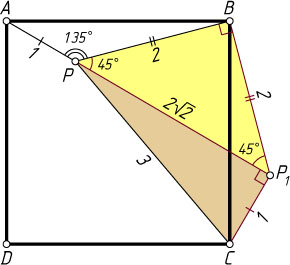
Автор: Курляндчик Л. Д.
Источник: Журнал «Квант». — 1983, № 4, с. 39, М796
Источник: Задачник «Кванта». — М796
Источник: Мерзляк А. Г., Поляков В. М. Геометрия. 9 класс. Углублённый уровень. — М.: Вентана-Граф, 2020. — № 22.33, с. 206
