6040. В выпуклом пятиугольнике ABCDE
углы ABC
и CDE
равны по 90^{\circ}
, стороны BC
, CD
и AE
равны по 1 и сумма сторон AB
и DE
равна 1. Докажите, что площадь пятиугольника равна 1.
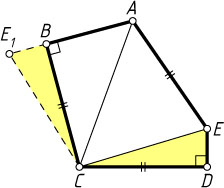
Указание. Поверните треугольник CDE
вокруг точки C
так, чтобы точка D
перешла в точку B
.
Решение. Повернём треугольник CDE
вокруг точки C
так, чтобы точка D
перешла в точку B
. Пусть при этом точка E
перешла в точку E_{1}
. Тогда точка E_{1}
лежит на прямой AB
,
AE_{1}=AB+BE_{1}=AB+DE=1,
S_{\triangle CAE_{1}}=\frac{1}{2}AE_{1}\cdot BC=1\cdot\frac{1}{2}=\frac{1}{2},
а так как треугольник CAE
равен треугольнику CAE_{1}
, то S_{\triangle CAE}=\frac{1}{2}
. Следовательно, площадь пятиугольника равна 1.
Автор: Произволов В. В.
Источник: Журнал «Квант». — 1991, № 11, с. 27, задача 5
Источник: Произволов В. В. Задачи на вырост. — М.: МИРОС, 1995. — № 2, с. 19
Источник: Журнал «Crux Mathematicorum». — 2003, № 5, задача 3, с. 263
