6044. В треугольнике ABC
угол B
равен 120^{\circ}
. Биссектриса угла ABC
пересекает сторону AC
в точке M
, а биссектриса угла, смежного с углом BCA
, пересекает продолжение стороны AB
в точке P
. Отрезок MP
пересекает сторону BC
в точке K
. Докажите, что угол AKM
равен 30^{\circ}
.
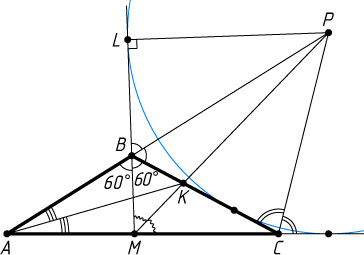
Решение. Пусть L
— точка на продолжении биссектрисы BM
за вершину B
. Тогда
\angle LBP=\angle ABM=60^{\circ}=\angle CBP,
поэтому BP
— биссектриса внешнего угла при вершине B
треугольника BMC
. По условию задачи CP
— биссектриса внешнего угла при вершине C
треугольника BMC
, а так как биссектрисы двух внешних и третьего внутреннего угла треугольника пересекаются в одной точке (центре вневписанной окружности), то MP
— биссектриса угла при вершине M
треугольника BMC
.
Биссектрисы BC
и MP
внешних углов при вершинах B
и M
треугольника ABM
пересекаются в точке K
, значит, AK
— биссектриса угла BAM
.
По теореме о внешнем угле треугольника
\angle AKM=\angle KMC-\angle KAC=\frac{1}{2}\angle BMC-\frac{1}{2}\angle BAC=
=\frac{1}{2}(\angle BMC-\angle BAC)=\frac{1}{2}\angle ABM=\frac{1}{2}\cdot60^{\circ}=30^{\circ}.
Что и требовалось доказать.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 761, с. 95
