6046. Диагонали четырёхугольника, вписанного в окружность с центром O
, пересекаются в точке Q
, M
и K
— середины диагоналей, N
и P
— проекции точек O
и Q
на прямую MK
. Известно, что ни одна из диагоналей не проходит через точку O
. Докажите, что MN=PK
.
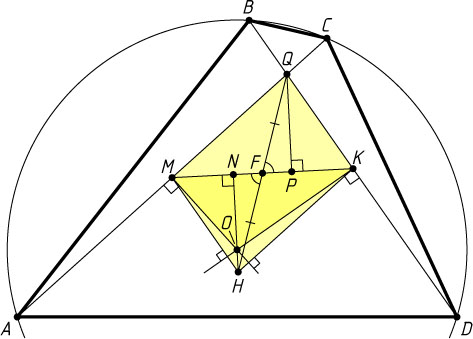
Решение. Первый способ. Пусть M
и K
— середины диагоналей соответственно AC
и BD
четырёхугольника ABCD
, вписанного в окружность с центром O
(рис. 1), а N
и P
— проекции точек соответственно Q
и O
на прямую MK
.
Пусть H
— точка пересечения высот треугольника MOK
. Тогда KH\perp OM
, а так как диаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде, то MQ\perp OM
. Значит, KH\parallel MQ
. Аналогично MH\parallel KQ
, поэтому QMHK
— параллелограмм. Точки P
и N
— проекции вершин H
и Q
этого параллелограмма на диагональ MK
.
Пусть F
— точка пересечения диагоналей параллелограмма QMHQ
. Прямоугольные треугольники QNF
и HPF
равны по гипотенузе и острому углу. Следовательно, MN=PK
.
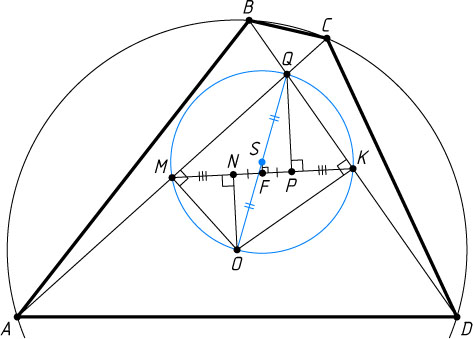
Второй способ. Пусть M
и K
— середины диагоналей соответственно AC
и BD
четырёхугольника ABCD
, вписанного в окружность с центром O
(рис. 2), а N
и P
— проекции точек соответственно Q
и O
на прямую MK
.
Диаметр окружности, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде, поэтому из точек M
и K
отрезок OQ
виден под прямым углом. Значит, эти точки лежат на окружности с диаметром OQ
и с центром в середине S
отрезка OQ
. Отрезок PN
— проекция диаметра OQ
на прямую MK
, значит, проекция середины S
этого диаметра — середина F
отрезка PN
.
С другой стороны, перпендикуляр, опущенный из центра S
окружности с диаметром OQ
на хорду KN
, также проходит через середину F
этой хорды, поэтому FM=FK
и FN=FP
. Следовательно, MN=|FM-FN|=|FK-FP|=PK
. Что и требовалось доказать.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 1003, с. 123

