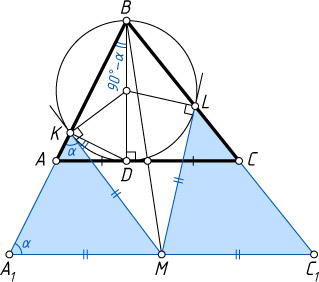
6062. На высоте BD
треугольника ABC
как на диаметре построена окружность, пересекающая стороны AB
и BC
соответственно в точках K
и L
. Прямые, касающиеся окружности в точках K
и L
, пересекаются в точке M
. Докажите, что прямая BM
делит сторону AC
пополам.
Решение. Пусть прямая, проходящая через точку M
параллельно AC
, пересекает прямые AB
и BC
в точках A_{1}
и C_{1}
соответственно. Докажем, что M
— середина отрезка A_{1}C_{1}
. Отсюда будет следовать утверждение задачи.
Обозначим \angle MKA_{1}=\alpha
. Тогда
\angle DKM=\angle DKA_{1}-\angle MKA_{1}=90^{\circ}-\alpha.
Из теоремы об угле между касательной и хордой следует, что
\angle DKM=\angle KBD=90^{\circ}-\angle BAD=90^{\circ}-\angle BA_{1}M,
откуда находим, что
\angle KA_{1}M=\angle BA_{1}M=90^{\circ}-\angle DKM=90^{\circ}-(90^{\circ}-\alpha)=\alpha=\angle MKA_{1}.
Следовательно, треугольник KMA_{1}
равнобедренный, MA_{1}=MK
. Аналогично MC_{1}=ML
, а так как MK=ML
как отрезки касательных, проведённых к окружности из одной точки, то MA_{1}=MC_{1}
. Что и требовалось доказать.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 480, с. 58
