6087. В сектор с центральным углом 60^{\circ}
и единичным радиусом вписан прямоугольник (все вершины на границе сектора). Чему равно наибольшее значение площади таких прямоугольников?
Ответ. \frac{\sqrt{3}}{6}
.
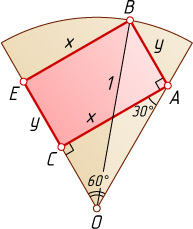
Решение. Рассмотрим два случая: а) вершины C
и E
прямоугольника ABEC
расположены на одном радиусе сектора, вершина A
— на другом, а вершина B
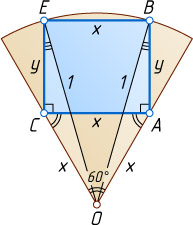
— на дуге сектора; б) вершины B
и E
прямоугольника ABEC
расположены на дуге сектора, а вершины A
и C
— на радиусах.
а) Обозначим AC=BE=x
, CE=AB=y
, S=xy
— площадь прямоугольника. Пусть O
— вершина центрального угла. Тогда
\angle OAB=120^{\circ},~OA=\frac{AC}{\sin60^{\circ}}=\frac{2x}{\sqrt{3}}.
Применив теорему косинусов к треугольнику OAB
, получим, что
OB^{2}=OA^{2}+AB^{2}-2OA\cdot AB\cos120^{\circ},~1=\frac{4}{3}x^{2}+y^{2}+2\cdot\frac{2x}{\sqrt{3}}\cdot y\cdot\frac{1}{2}.
Тогда
1=\frac{4}{3}x^{2}+y^{2}+\frac{2xy}{\sqrt{3}}\geqslant2\sqrt{\frac{4}{3}x^{2}\cdot y^{2}}+\frac{2xy}{\sqrt{3}}=\frac{4xy}{\sqrt{3}}+\frac{2xy}{\sqrt{3}}=\frac{6xy}{\sqrt{3}}=\frac{6}{\sqrt{3}}S,
откуда S\leqslant\frac{\sqrt{3}}{6}
, причём равенство достигается, если \frac{4}{3}x^{2}=y^{2}
, т. е. при y=\frac{2x}{\sqrt{3}}
. Тогда x=\frac{1}{2}
, y=\frac{1}{\sqrt{3}}
.
б) Докажем, что в этом случае OA=OC
. Действительно, треугольник BOE
равнобедренный, поэтому \angle OBE=\angle OEB
. Тогда \angle OBA=\angle OEC
, значит, треугольники OBA
и OEC
равны по двум сторонам и углу между ними. Следовательно, OA=OC
. Что и требовалось доказать.
Таким образом, OAC
— равносторонний треугольник. В треугольнике AOB
известно, что
OA=AC=x,~AB=y,~OB=1,~\angle OAB=90^{\circ}+60^{\circ}=150^{\circ}.
На этот раз
1=x^{2}+y^{2}+xy\sqrt{3}\geqslant2\sqrt{x^{2}y^{2}}+xy\sqrt{3}=2xy+xy\sqrt{3}=xy(2+\sqrt{3})=S(2+\sqrt{3}),
откуда S\leqslant\frac{1}{2+\sqrt{3}}=2-\sqrt{3}
, причём равенство достигается, если x=y
, т. е. когда прямоугольник — квадрат со стороной \sqrt{2-\sqrt{3}}
.
Поскольку
\frac{\sqrt{3}}{6}\gt2-\sqrt{3}~\Leftrightarrow~\frac{7\sqrt{3}}{6}\gt2~\Leftrightarrow~7\sqrt{3}\gt12~\Leftrightarrow~147\gt144,
наибольшая площадь равна \frac{\sqrt{3}}{6}
.
Источник: Шарыгин И. Ф. Геометрия: 9—11 кл.: От учебной задачи к творческой: Учебное пособие. — М.: Дрофа, 1996. — № 833, с. 102

