6106. Четырёхугольник ABCD
вписан в окружность с диаметром AC
. Точки K
и M
— проекции вершин A
и C
соответственно на прямую BD
. Через точку K
проведена прямая, параллельная BC
и пересекающая AC
в точке P
. Докажите, что угол KPM
— прямой.
Решение. Пусть диагонали четырёхугольника ABCD
пересекаются в точке E
, а прямая, проходящая через точку K
параллельно BC
, пересекает диагональ AC
в точке P
, расположенной между C
и E
. Тогда
\angle PKD=\angle CBD=\angle CAD=\angle PAD,
значит, из точек K
и A
, лежащих по одну сторону от прямой PD
, отрезок PD
виден под одним и тем же углом, поэтому точки A
, K
, P
и D
лежат на одной окружности, а так как AK\perp BD
, то AD
— диаметр этой окружности, значит, \angle CPD=\angle APD=90^{\circ}
.
Из точек P
и M
отрезок CD
виден под прямым углом, значит, эти точки лежат на окружности с диаметром CD
. Тогда
\angle MPA=180^{\circ}-\angle CPM=\angle CDM=\angle CDB=\angle CAB,
поэтому PM\parallel AB
, а так как PK\parallel BC
и AB\perp BC
, то PM\perp PK
, что и требовалось доказать. Аналогично для случая, когда точка P
расположена между A
и E
.
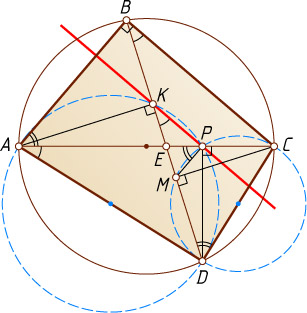
Автор: Емельянова Т. Л.
Источник: Всероссийская олимпиада школьников. — 2009-10, XXXVI, региональный этап, 11 класс
Источник: Журнал «Квант». — 2010, № 2, с. 55
