6111. Докажите, что при инверсии окружность, проходящая через центр инверсии, переходит в прямую, не проходящую через центр инверсии.
Решение. Рассмотрим инверсию относительно окружности S
радиуса R
с центром O
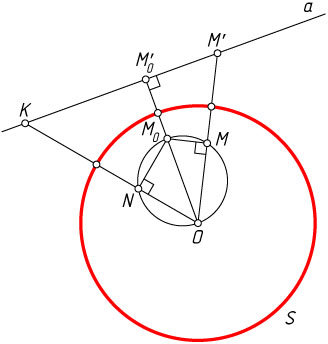
. Пусть M_{0}
— произвольная точка, отличная от O
, M_{0}'
— образ точки M_{0}
при рассматриваемой инверсии, a
— прямая, проходящая через точку M_{0}'
перпендикулярно OM_{0}'
, M
— произвольная точка окружности с диаметром OM_{0}
, отличная от O
и M_{0}
, M'
— образ точки M
. Тогда \angle OMM_{0}=90^{\circ}
, OM_{0}'=\frac{R^{2}}{OM_{0}}
и OM'=\frac{R^{2}}{OM}
, значит, \frac{OM_{0}'}{OM'}=\frac{OM}{OM_{0}}
, поэтому треугольник OM_{0}'M'
подобен прямоугольному треугольнику OMM_{0}
(угол при вершине O
— общий). Следовательно, \angle OM_{0}'M'=90^{\circ}
и точка M'
лежит на прямой a
.
Доказано, что при инверсии образы всех точек окружности, проходящей через центр инверсии, лежат на прямой a
, не проходящей через центр инверсии. Осталось доказать, что каждая точка прямой a
, является образом некоторой точки этой окружности.
Действительно, если K
— произвольная точка прямой a
, отличная от M_{0}'
, а луч OK
пересекает окружность с диаметром OM_{0}
в точке N
, то прямоугольные треугольники ONM_{0}
и OM_{0}'K
подобны по двум углам, поэтому \frac{ON}{OM_{0}'}=\frac{OM_{0}}{OK}
, откуда OK=\frac{OM_{0}\cdot OM_{0}'}{ON}=\frac{R^{2}}{ON}
. Следовательно, K
— образ точки N
при рассматриваемой инверсии. Что и требовалось доказать.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — с. 177
Источник: Курант Р., Роббинс Г. Что такое математика?. — 2-е изд. — М.: Просвещение, 1976. — с. 172
Источник: Костовский А. Н. Геометрические построения одним циркулем на плоскости и одним лишь сферографом в пространстве. — (Популярные лекции по математике. Вып. 29). — 3-е изд., перераб. и доп. — М.: Наука, 1989. — с. 29
Источник: Бакельман И. Я. Инверсия. — (Популярные лекции по математике. Вып. 44). — М.: Наука, 1966. — с. 19
Источник: Жижилкин И. Д. Инверсия. — (Библиотека «Математическое просвещение». Вып. 35). — М.: МЦНМО, 2009. — с. 10
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 256
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 28.3, с. 518
