6113. С помощью циркуля и линейки постройте образ данной точки при инверсии относительно данной окружности.
Решение. Первый способ. Рассмотрим инверсию относительно окружности с центром O
радиуса R
. Пусть M
— произвольная точка плоскости.
Если точка M
лежит на окружности инверсии, то её образом будет сама точка M
.
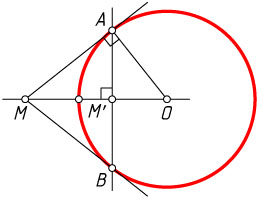
Если точка M
лежит вне окружности инверсии (рис. 1), проведём через неё касательные к окружности инверсии. Пусть A
и B
— точки касания. Тогда точка пересечения M'
отрезка OM
с хордой AB
и есть искомая точка.
Действительно, поскольку OA\perp AM
и AM'\perp OM
, отрезок AM'
— высота прямоугольного треугольника, проведённая из вершины прямого угла, значит, OM'\cdot OM=OA^{2}=R^{2}
. Следовательно, OM'=\frac{R^{2}}{OM}
, а это и означает, что M'
— образ точки M
при симметрии относительно окружности с центром O
радиуса R
.
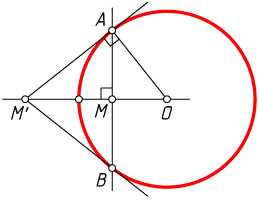
Если же точка M
лежит внутри окружности инверсии и отлична от O
(рис. 2), то проведём через M
хорду AB
, перпендикулярную OM
, и через точку A
касательную к окружности инверсии. Пересечение этой касательной с прямой OM
и есть искомая точка. Доказательство аналогично доказательству для предыдущего случая.
Второй способ. Пусть O
— центр окружности S
радиуса R
, A
— произвольная точка, не лежащая на окружности (рис. 3). Через точку A
проведём прямую OA
и секущую AKM
. Пусть N
— точка, симметричная точке M
относительно прямой OA
. Тогда для точки B
пересечения прямых NK
и прямой AO
верно равенство OB\cdot OA=R^{2}
(см. задачу 10671). Следовательно, B
— образ точки A
при инверсии относительно окружности S
.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — с. 204
Источник: Жижилкин И. Д. Инверсия. — (Библиотека «Математическое просвещение». Вып. 35). — М.: МЦНМО, 2009. — с. 5
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 28.9, с. 518

