6114. Докажите, что если окружность и прямая (либо две окружности) касаются в точке M
, отличной от точки O
, то их образы при инверсии относительно окружности с центром O
также касаются, а при инверсии с центром M
окружность и прямая (две окружности) переходят в две параллельные прямые.
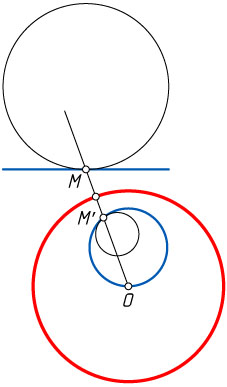
Решение. Пусть точка M
не совпадает с центром инверсии (рис. 1). Прямая, не проходящая через центр инверсии, переходит в окружность, а окружность, не проходящая через центр инверсии, — также в окружность, поэтому, если M
— единственная общая точка прямой и окружности (или двух окружностей), то её образ M'
— единственная общая точка образов прямой и окружности (или двух окружностей).
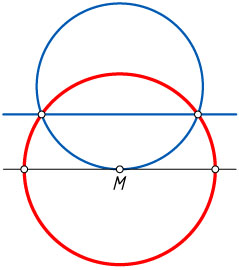
Пусть теперь точка M
— центр инверсии (рис. 2). Прямая, проходящая через центр инверсии, переходит в себя, а окружность, проходящая через центр инверсии, — в прямую, не проходящую через центр инверсии. Точка M
при этом переходит в бесконечно удалённую точку. Следовательно, образы прямой и окружности (или двух окружностей) — прямые, не имеющие ни одной общей точки, т. е. параллельные прямые.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — с. 182
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 28.4, с. 518

