6115. Докажите, что при инверсии сохраняется угол между окружностями (между окружностью и прямой, между прямыми).
Решение. Пусть прямые l_{1}
и l_{2}
пересекаются в точке O
. При инверсии относительно окружности с центром O
каждая из этих прямых переходит в себя, значит, угол между ними сохраняется.
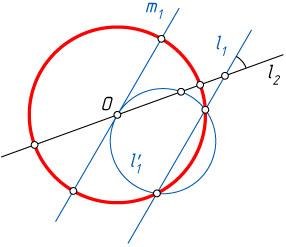
Если прямые пересекаются в точке M
, отличной от центра O
инверсии (рис. 1), а центр инверсии лежит на одной из прямых (например, на l_{2}
), то прямая l_{2}
переходит в себя, а прямая l_{1}
— в окружность l_{1}'
, проходящую через центр инверсии.
Пусть m_{1}
— касательная к этой окружности в точке O
. Если ещё раз применить ту же инверсию, то окружность l_{1}'
перейдёт в прямую l_{1}
, а прямая m_{1}
— в себя, так как она проходит через центр инверсии. В то же время, O
— точка касания прямой m_{1}
и окружности l_{1}'
, значит, при инверсии с центром O
они перейдут в пару параллельных прямых, поэтому m_{1}\parallel l_{1}
. Следовательно, угол между прямой l_{2}'
(совпадающей с l_{2}
) и касательной m_{1}
к окружности l_{1}'
равен углу между прямыми l_{1}
и l_{2}
.
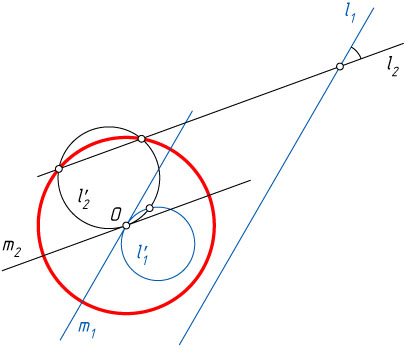
Пусть центр инверсии не лежит ни на одной из прямых l_{1}
и l_{2}
(рис. 2). Тогда образы этих прямых — окружности l_{1}'
и l_{2}'
, проходящие через центр инверсии.
Пусть m_{1}
и m_{2}
— касательные к этим окружностям в точке O
. Если ещё раз применить ту же инверсию, то окружность l_{1}'
и касательная к ней m_{1}
перейдут в пару параллельных прямых l_{1}
и m_{1}
, а окружность l_{2}'
и касательная к ней m_{2}
— в пару параллельных прямых l_{2}
и m_{2}
. Следовательно, угол между окружностями l_{1}'
и l_{2}'
равен углу между прямыми l_{1}
и l_{2}
.
Аналогично доказывается, что при инверсии сохраняется угол между окружностью и прямой.
Источник: Яглом И. М. Геометрические преобразования. — Т. 2: Линейные и круговые преобразования. — М.: ГИТТЛ, 1956. — с. 181
Источник: Бакельман И. Я. Инверсия. — (Популярные лекции по математике. Вып. 44). — М.: Наука, 1966. — с. 22-24
Источник: Жижилкин И. Д. Инверсия. — (Библиотека «Математическое просвещение». Вып. 35). — М.: МЦНМО, 2009. — с. 18
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — с. 259
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 28.5, с. 518

