6133. На продолжениях сторон AB
, BC
, CD
и DA
выпуклого четырёхугольника ABCD
за точки B
, C
, D
и A
соответственно отложены отрезки BB_{1}
, CC_{1}
, DD_{1}
и AA_{1}
, равные этим сторонам. Найдите площадь четырёхугольника A_{1}B_{1}C_{1}D_{1}
, если площадь четырёхугольника ABCD
равна s
.
Ответ. 5s
.
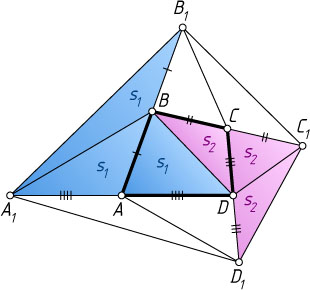
Решение. Обозначим S_{\triangle ABD}=s_{1}
, S_{\triangle BCD}=s_{2}
. Отрезки AB
и A_{1}B
— медианы треугольников A_{1}BD
и AA_{1}B_{1}
, поэтому
S_{\triangle A_{1}BB_{1}}=S_{\triangle A_{1}AB}=S_{\triangle ABD}=s_{1},
значит, S_{\triangle AA_{1}B_{1}}=2s_{1}
. Аналогично, S_{\triangle CD_{1}C_{1}}=2s_{2}
, поэтому
S_{\triangle AA_{1}B_{1}}+S_{\triangle CD_{1}C_{1}}=2s_{1}+2s_{2}=2(s_{1}+s_{2})=2s.
Аналогично получим, что
S_{\triangle BB_{1}C_{1}}+S_{\triangle DA_{1}D_{1}}=2s.
Следовательно,
S_{A_{1}B_{1}C_{1}D_{1}}=S_{\triangle AA_{1}B_{1}}+S_{\triangle CD_{1}C_{1}}+S_{\triangle BB_{1}C_{1}}+S_{\triangle DA_{1}D_{1}}+S_{ABCD}=2s+2s+s=5s.
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 4.5, с. 82
Источник: Васильев Н. Б., Егоров А. А. Задачи всесоюзных математических олимпиад. — М.: Наука, 1988. — № 13, с. 23
Источник: Математические олимпиады ЮАР. — 1995
Источник: Журнал «Crux Mathematicorum». — 2001, № 8, задача 1, с. 489
