6134. Перпендикуляры, опущенные из внутренней точки равностороннего треугольника, на его стороны, и отрезки, соединяющие эту точку с вершинами, разбивают треугольник на шесть прямоугольных треугольников. Докажите, что сумма площадей трёх из них, взятых через один, равна сумме площадей трёх остальных.
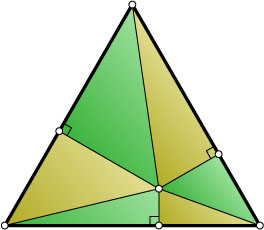
Указание. Через данную точку проведите прямые, параллельные сторонам треугольника.
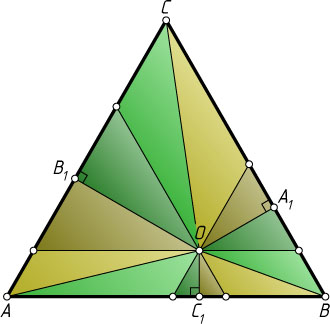
Решение. Пусть A_{1}
, B_{1}
и C_{1}
— основания перпендикуляров, опущенных из внутренней точки O
равностороннего треугольника ABC
на его стороны BC
, AC
и AB
соответственно.
Через точку O
проведём прямые, соответственно параллельные сторонам треугольника. Эти прямые разбивают треугольник ABC
на три равносторонних треугольника и три параллелограмма. Отрезки OA
, OB
и OC
— диагонали параллелограммов, значит, они разбивают параллелограммы на равные треугольники. Отрезки OA_{1}
, OB_{1}
и OC_{1}
— высоты соответствующих равносторонних треугольников, значит, они также разбивают эти треугольники на равные треугольники. Отсюда следует решение задачи.
Источник: Произволов В. В. Задачи на вырост. — М.: МИРОС, 1995. — № 2, с. 53

