6143. Окружность радиуса 3 проходит через вершину B
, середины сторон AB
и BC
, а также касается стороны AC
треугольника ABC
. Угол BAC
— острый, и \sin\angle BAC=\frac{1}{3}
. Найдите площадь треугольника ABC
.
Ответ. 16\sqrt{2}
.
Решение. Пусть M
и N
— середины сторон BC
и AB
соответственно, K
— точка касания описанной окружности треугольника BMN
со стороной AC
, O
— центр окружности, R=3
— её радиус. Отрезок MN
— средняя линия треугольника ABC
, поэтому MN\parallel AC
, значит, \angle BNM=\angle BAC
. По теореме синусов
BM=2R\sin\angle BNM=2R\sin\angle BAC=2\cdot3\cdot\frac{1}{3}=2,~BC=2BM=4.
По теореме о касательной секущей
CK=\sqrt{BC\cdot CM}=\sqrt{4\cdot2}=2\sqrt{2}.
Пусть P
— основание перпендикуляра, опущенного из центра O
окружности на прямую BC
. Тогда P
— середина BM
, поэтому MP=BP=1
и CP=CM+MP=2+1=3
. Из прямоугольного треугольника BOP
находим, что
OP=\sqrt{OB^{2}-BP^{2}}=\sqrt{9-1}=2\sqrt{2}.
Прямоугольные треугольники OKC
и CPO
равны по двум катетам (OK=CP=3
и CK=OP=2\sqrt{2}
), поэтому \angle COK=\angle OCP
, а так как \angle KCO=90^{\circ}-\angle COK
, то \angle OCP+\angle KCO=90^{\circ}
. Таким образом, треугольник ABC
— прямоугольный. Тогда
AB=\frac{BC}{\sin\angle BAC}=\frac{4}{\frac{1}{3}}=12,~AC=\sqrt{12^{2}-4^{2}}=8\sqrt{2}.
Следовательно,
S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}\cdot8\sqrt{2}\cdot4=16\sqrt{2}.
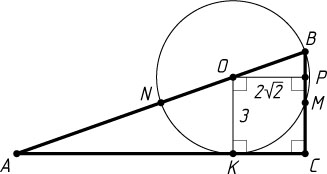
Источник: Вступительный экзамен на механико-математический факультет МГУ. — 1974, № 3, вариант 4
