6167. Прямая, перпендикулярная боковой стороне равнобедренного треугольника отсекает от него четырёхугольник, в который можно вписать окружность. Найдите радиус окружности, если отрезок прямой, заключённый внутри треугольника, равен 6, а отношение боковой стороны треугольника к его основанию равно \frac{5}{6}
.
Ответ. 5{,}25
или 4{,}5
.
Решение. Заметим, что окружность, вписанная в четырёхугольник, о котором говорится в условии задачи, — это окружность вписанная в данный равнобедренный треугольник.
Пусть вписанная окружность равнобедренного треугольника ABC
касается боковой стороны AB
в точке D
, основания BC
— в точке E
. Тогда AE
— высота и медиана треугольника ABC
. Обозначим \angle ABC=\alpha
. Тогда
\cos\alpha=\frac{BE}{AB}=\frac{\frac{1}{2}BC}{AB}=\frac{1}{2}\cdot\frac{6}{5}=\frac{3}{5},
\sin\alpha=\frac{4}{5},~\tg\alpha=\frac{4}{3},~\tg\angle BAC=\tg(180^{\circ}-2\alpha)=
=\frac{2\tg\alpha}{\tg^{2}\alpha-1}=\frac{2\cdot\frac{4}{3}}{\frac{16}{9}-1}=\frac{24}{7}.
Пусть O
— центр этой окружности, r
— её радиус. Тогда
AO=\frac{OD}{\cos\angle AOD}=\frac{r}{\cos\alpha}=\frac{r}{\frac{3}{5}}=\frac{5}{3}r,~AD=OD\tg\alpha=r\cdot\frac{4}{3}=\frac{4}{3}r.
AE=AO+OE=\frac{5}{3}r+r=\frac{8}{3}r,~BD=BE=AE\cdot\ctg\alpha=\frac{8}{3}r\cdot\frac{3}{4}=2r.
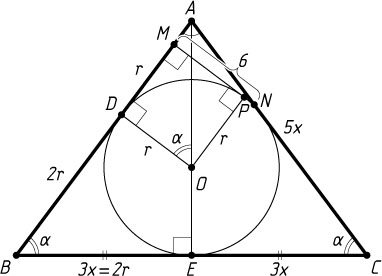
Предположим, что прямая, проходящая через точку M
, лежащую на прямой, содержащей боковую сторону AB
, перпендикулярна AB
, касается окружности в точке P
и пересекает боковую сторону AC
в точке N
(рис. 1). Четырёхугольник ODMP
— квадрат со стороной r
, поэтому
DM=OP=r,~AM=\frac{MN}{\tg\angle MAN}=\frac{6}{\frac{24}{7}}=\frac{7}{4},
AB=AM+MD+BD=\frac{7}{4}+r+2r=\frac{7}{4}+3r,
а так как
AB=\frac{BE}{\cos\alpha}=\frac{2r}{\frac{3}{5}}=\frac{10}{3}r,
то \frac{7}{4}+3r=\frac{10}{3}r
. Следовательно, r=\frac{21}{4}
.
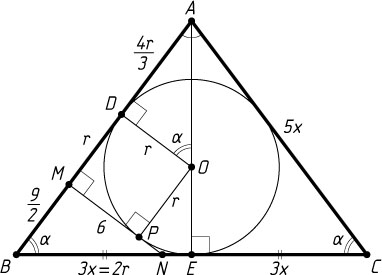
Пусть теперь прямая, проходящая через точку M
, лежащую на боковой стороне AB
, перпендикулярна AB
, касается окружности в точке P
и пересекает основание BC
в точке N
(рис. 2). Тогда
BM=\frac{MN}{\tg\alpha}=\frac{6}{\frac{4}{3}}=\frac{9}{2},~AB=BM+MD+AD=\frac{9}{2}+r+\frac{4}{3}r=\frac{9}{2}+\frac{7}{3}r,
а так как AB=\frac{10}{3}r
, то \frac{9}{2}+\frac{7}{3}r=\frac{10}{3}r
. Следовательно, r=\frac{9}{2}
.
Если же точка M
лежит на боковой стороне AC
, получим те же результаты.
Источник: ЕГЭ. — Задача C4, 2011
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 21, с. 175

