6194. Две стороны треугольника равны 6 и 12, косинус угла между ними равен \frac{1}{4}
. В треугольник вписан ромб, имеющий с треугольником общий угол (вершина ромба, противоположная вершине этого угла, лежит на третьей стороне треугольника). Найдите сторону ромба.
Ответ. 4
или 6
.
Решение. Пусть в треугольнике ABC
известно, что AB=12
, AC=6
, \angle BAC=\alpha
, \cos\alpha=\frac{1}{4}
. По теореме косинусов
BC=\sqrt{AB^{2}+AC^{2}-2AB\cdot AC\cos\alpha}=\sqrt{144+36-2\cdot12\cdot6\cdot\frac{1}{4}}=12,
значит, треугольник ABC
— равнобедренный, BC=AB=12
.
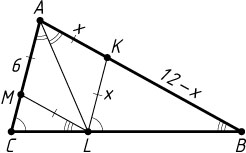
Рассмотрим случай, когда общий угол треугольника и ромба — это угол при вершине A
(рис. 1). Пусть AKLM
— ромб со стороной x
, причём вершина L
ромба лежит на стороне BC
треугольника ABC
, а вершина M
— на стороне AC
. Треугольники KBL
и ABC
подобны, так как KL\parallel AC
, значит, \frac{KL}{AC}=\frac{BK}{AB}
, или \frac{x}{6}=\frac{12-x}{12}
. Из этого уравнения находим, что x=4
.
В случае, когда C
— общий угол ромба и треугольника, получим тот же результат.
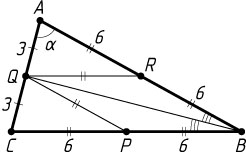
Предположим теперь, что общий угол треугольника и ромба — это угол при вершине B
(рис. 2). Пусть BPQR
— ромб, причём вершина Q
ромба лежит на основании AC
треугольника ABC
, а вершина R
— на стороне AB
. Точка Q
— середина AC
(так как BQ
— биссектриса, а значит, и медиана равнобедренного треугольника ABC
) и QR\parallel BC
, поэтому QR
— средняя линия треугольника ABC
. Следовательно, QR=\frac{1}{2}BC=6
.
Источник: ЕГЭ. — Задача C4, 2011
Источник: Гордин Р. К. ЕГЭ 2013. Математика. Задача C4. Геометрия. Планиметрия. — М.: МЦНМО, 2014. — № 14.35, с. 139
Источник: Гордин Р. К. ЕГЭ 2017. Математика. Геометрия. Стереометрия. Задача 14 (профильный уровень). — М.: МЦНМО, 2017. — № 14.35.1, с. 142

