6199. Через вершину C
правильного шестиугольника ABCDEF
проведена прямая, пересекающая прямую AD
в точке Q
. Известно, что эта прямая разбивает шестиугольник на части, площади которых относятся как 5:13
. Найдите отношение AQ:QD
.
Ответ. 2:1
или 1:3
.
Решение. Пусть O
— центр правильного шестиугольника ABCDEF
, S
— его площадь, K
— точка пересечения диагоналей AD
и CE
. Площади частей, на которые прямая CQ
разбивает шестиугольник, равны \frac{5}{18}S
и \frac{13}{18}S
.
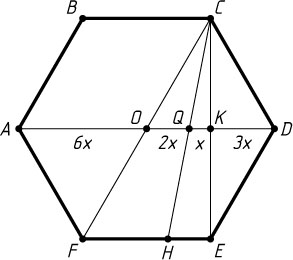
Предположим, что точка D
— вершина меньшей по площади части шестиугольника (рис. 1). Тогда точка Q
лежит между точками O
и D
, так как
S_{\triangle CDE}=S_{\triangle COD}=\frac{1}{6}S\lt\frac{5}{18}S,S_{CDEF}=\frac{1}{2}S\gt\frac{5}{18}S,
значит, прямая CP
пересекает сторону EF
в некоторой точке H
. При этом
S_{\triangle CEH}=S_{CDEH}-S_{\triangle CDE}=\frac{5}{18}S-\frac{1}{6}S=\frac{1}{9}S=\frac{1}{3}\cdot\frac{1}{3}S=\frac{1}{3}S_{\triangle CEF},
т. е. площадь треугольника CEH
в три раза меньше площади треугольника CEF
, значит, EH=\frac{1}{3}EF
, а так как OK\parallel EF
, то QK=\frac{1}{3}OK
.
Обозначим QK=x
. Тогда
KD=OK=3x,~QD=QK+KD=x+3x=4x,
AO=OD=2OK=6x,~AQ=AO+OQ=6x+2x=8x,
следовательно, \frac{AQ}{QD}=\frac{8x}{4x}=2
.
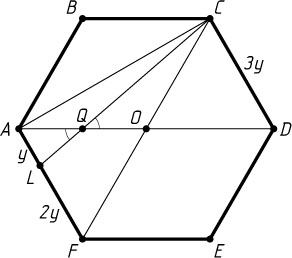
Пусть теперь точка D
— вершина большей по площади части шестиугольника (рис. 2). Аналогично предыдущему случаю докажем, что тогда точка Q
лежит между точками A
и O
, значит, прямая CQ
пересекает сторону AF
в некоторой точке L
и при этом площадь треугольника CAL
в три раза меньше площади треугольника CAF
, значит, AL=\frac{1}{3}AF=\frac{1}{3}CD
.
Треугольник AQL
подобен треугольнику DQC
с коэффициентом \frac{1}{3}
(AL\parallel CD
), следовательно, \frac{AQ}{QD}=\frac{1}{3}
.
Источник: ЕГЭ. — Задача C4, 2011

