6200. Через точку S
, лежащую вне окружности с центром O
, проведены две касательные, касающиеся окружности в точках A
и B
, и секущая, пересекающая окружность в точках M
и N
. Прямые AB
и SO
пересекаются в точке K
. Докажите, что точки M
, N
, K
и O
лежат на одной окружности.
Указание. Докажите, что SM\cdot SN=SO\cdot SK
.
Решение. По теореме о касательной и секущей SM\cdot SN=SA^{2}
. С другой стороны, поскольку AK
— высота прямоугольного треугольника OAS
, проведённая из вершины прямого угла, то SA^{2}=SO\cdot SK
. Следовательно, SM\cdot SN=SO\cdot SK
, а это означает, что точки M
, N
, K
и O
лежат на одной окружности (см. задачу 114).
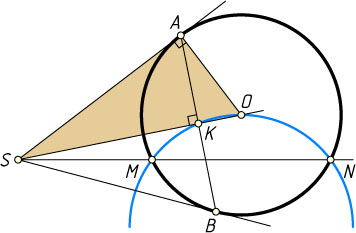
Источник: Московская областная математическая олимпиада. — 1993-94, 10 класс.
Источник: Понарин Я. П. Элементарная геометрия. — Т. 1: Планиметрия, преобразования плоскости. — М.: МЦНМО, 2004. — № 2.22, с. 24
