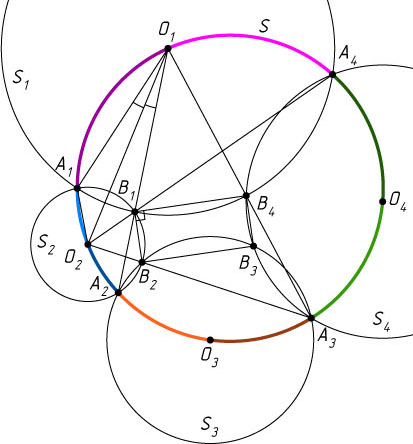
6201. Центры четырёх окружностей S_{1}
, S_{2}
, S_{3}
и S_{4}
лежат на окружности S
. Окружности S_{1}
и S_{2}
пересекаются в точках A_{1}
и B_{1}
, S_{2}
и S_{3}
— в точках A_{2}
и B_{2}
, S_{3}
и S_{4}
— в точках A_{3}
и B_{3}
, окружности S_{4}
и S_{1}
— в точках A_{4}
и B_{4}
, причём точки A_{1}
, A_{2}
, A_{3}
и A_{4}
лежат на окружности S
, а точки B_{1}
, B_{2}
, B_{3}
и B_{4}
различны и лежат внутри S
. Докажите, что B_{1}B_{2}B_{3}B_{4}
— прямоугольник.
Решение. Пусть O_{1}
, O_{2}
, O_{3}
и O_{4}
— центры окружностей S_{1}
, S_{2}
, S_{3}
и S_{4}
соответственно. Покажем, что точка B_{1}
лежит на прямой O_{1}A_{2}
.
Треугольники B_{1}O_{1}O_{2}
и A_{1}O_{1}O_{2}
равны по трём сторонам, поэтому \angle B_{1}O_{1}O_{2}=\angle A_{1}O_{1}O_{2}
. С другой стороны, \angle A_{2}O_{1}O_{2}=\angle A_{1}O_{1}O_{2}
как вписанные в окружность S
углы, опирающиеся на равные дуги O_{2}A_{1}
и O_{2}A_{2}
. Значит, \angle B_{1}O_{1}O_{2}=\angle A_{2}O_{1}O_{2}
. Следовательно, точка B_{1}
лежит на прямой O_{1}A_{2}
.
Аналогично, B_{4}
лежит на прямой O_{1}A_{3}
, B_{2}
— на прямой O_{2}A_{3}
, B_{1}
— на прямой O_{2}A_{4}
.
Докажем, что \angle B_{4}B_{1}B_{2}=90^{\circ}
. Действительно,
\angle B_{4}B_{1}B_{2}=360^{\circ}-\angle B_{4}B_{1}O_{1}-\angle O_{1}B_{1}O_{2}-\angle O_{2}B_{1}B_{2}=
=360^{\circ}-\frac{1}{2}(180^{\circ}-\angle B_{1}O_{1}B_{4})-\angle O_{1}A_{1}O_{2}-\frac{1}{2}(180^{\circ}-\angle B_{1}O_{2}B_{2})=
=180^{\circ}+\frac{1}{2}(\angle B_{1}O_{1}B_{4}+\angle B_{1}O_{2}B_{2})-\angle O_{1}A_{1}O_{2}.
В то же время
\angle B_{1}O_{1}B_{4}+\angle B_{1}O_{2}B_{2}=\angle A_{3}O_{1}O_{2}-\angle B_{1}O_{1}O_{2}+\angle A_{3}O_{2}O_{1}-\angle B_{1}O_{2}O_{1}=
=180^{\circ}-\angle O_{1}A_{3}O_{2}-(180^{\circ}-\angle O_{1}B_{1}O_{2})=
=\angle O_{1}A_{1}O_{2}-(180^{\circ}-\angle O_{1}A_{1}O_{2})=2\angle O_{1}A_{1}O_{2}-180^{\circ}.
Поэтому
\angle B_{4}B_{1}B_{2}=180^{\circ}+\frac{1}{2}(2\angle O_{1}A_{1}O_{2}-180^{\circ})-\angle O_{1}A_{1}O_{2}=90^{\circ}.
Аналогично докажем, что и другие углы четырёхугольника B_{1}B_{2}B_{3}B_{4}
прямые.
Источник: Московская областная математическая олимпиада. — 1993-94, 11 класс.
