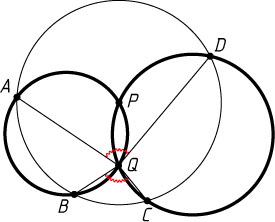
6209. Две окружности пересекаются в точках P
и Q
. Третья окружность с центром в точке P
пересекает первую в точках A
и B
, а вторую — в точках C
и D
(см.рис.). Докажите что углы AQD
и BQC
равны.
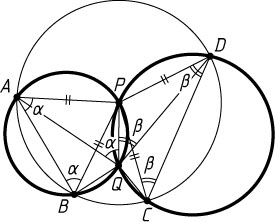
Решение. Треугольники APB
и DPC
равнобедренные. Обозначим углы при их основаниях
\angle ABP=\angle BAP=\alpha,~\angle DCP=\angle CDP=\beta.
Докажем, что \angle AQD=\alpha+\beta
и \angle BQC=\alpha+\beta
.
Вписанные углы AQP
и ABP
опираются на одну и ту же дугу, поэтому
\angle AQP=\angle ABP=\alpha.
Аналогично,
\angle DQP=\angle DCP=\beta.
Тогда
\angle AQD=\angle AQP+\angle DQP=\alpha+\beta.
Кроме того,
\angle BQP=\angle BAP=\alpha,~\angle CQP=\beta,
\angle BQC=\angle BQP+\angle CQP=\alpha+\beta.
Следовательно, \angle AQD=\angle BQC
.
Примечание. Во избежание рассмотрения случаев эта задача предлагалась участникам олимпиады только для расположения точек, указанного на рисунке. Тем не менее, утверждение верно всегда.
Автор: Заславский А. А.
Источник: Московская математическая олимпиада. — 1999, LXII, 10 класс
Источник: Журнал «Квант». — 1999, № 4, с. 18, М1693; 2000, № 1, с. 22, М1693
Источник: Задачник «Кванта». — М1693
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 2, с. 42

