6210. Хорды AC
и BD
окружности с центром O
пересекаются в точке K
. Пусть M
и N
— центры окружностей, описанных около треугольников AKB
и CKD
соответственно. Докажите, что OM=KN
.
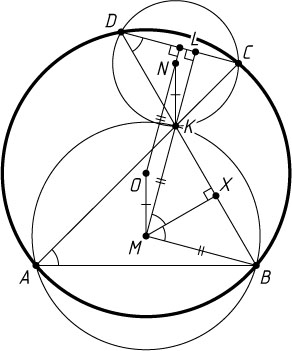
Решение. Пусть X
— проекция точки M
на BK
(рис. 1). Поскольку BMK
— центральный угол описанной окружности треугольника AKB
, а BAK
— угол, вписанный в эту окружность, то
\angle BAK=\frac{1}{2}\angle BMK=\angle KMX.
С другой стороны, BAC
и BDC
— углы, вписанные в окружность с центром O
, поэтому
\angle KDC=\angle BDC=\angle BAC=\angle BAK.
Значит, \angle KDC=\angle KMX
.
Если прямые MK
и DC
пересекаются в точке L
, то два угла треугольника DKL
соответственно равны двум углам треугольника MKX
, поэтому
\angle DLK=\angle MXK=90^{\circ},
т. е. MK\perp CD
.
Прямая ON
— линия центров окружности с центром O
и описанной окружности треугольника CKD
, а CD
— общая хорда этих окружностей, поэтому ON\perp CD
. Таким образом прямые MK
и ON
либо параллельны, либо совпадают, поскольку они перпендикулярны одной и той же прямой CD
.
Аналогично для прямых NK
и OM
. Следовательно, если точки O
, K
, M
и N
не лежат на одной прямой, то OMKN
— параллелограмм, и OM=KN
.
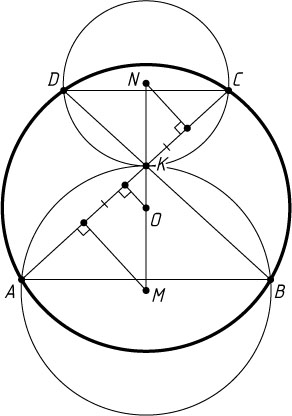
Пусть теперь точки O
, K
, M
и N
лежат на одной прямой (рис. 2). Рассмотрим проекции отрезков OM
и KN
на прямую AC
. Поскольку точки O
, M
и N
проектируются соответственно в середины отрезков AC
, AK
и KC
, то проекции отрезков OM
и KN
равны \frac{1}{2}KC
, а так как эти отрезки лежат на одной прямой, то из равенства проекций следует равенство самих отрезков.
Автор: Заславский А. А.
Источник: Московская математическая олимпиада. — 2000, LXIII, 11 класс
Источник: Фёдоров Р. М. и др. Московские математические олимпиады. 1993—2005 / Под ред. В. М. Тихомирова. — М.: МЦНМО, 2006. — № 3, с. 47

