6240. На сторонах AB
и BC
остроугольного треугольника ABC
построены как на основаниях равнобедренные треугольники AFB
и BLC
, причём один из них лежит внутри треугольника ABC
, а другой построен во внешнюю сторону. При этом \angle AFB=\angle BLC
и \angle CAF=\angle ACL
. Докажите, что прямая FL
отсекает от угла ABC
равнобедренный треугольник.
Решение. Обозначим \angle BAC=\alpha
, \angle ACB=\gamma
. Для определённости будем считать, что вершины A
, B
и C
треугольника ABC
ориентированы по часовой стрелке и \alpha\geqslant\gamma
. Тогда треугольник AFB
отложен во внутреннюю сторону, треугольник BLC
— во внешнюю.
Заметим, что равнобедренные треугольники AFB
и BLC
подобны. Обозначим через \varphi
углы при их основаниях. Тогда по условию
\alpha-\varphi=\angle CAF=\angle ACL=\gamma+\varphi,
откуда \varphi=\frac{\alpha-\gamma}{2}
.
Треугольник BAC
переходит в треугольник BFL
при поворотной гомотетии с центром B
, коэффициентом \frac{BF}{BA}=\frac{BL}{BC}
и углом поворота \varphi
против часовой стрелки. Значит, (ориентированная) прямая FL
получается из (ориентированной) прямой AC
поворотом на угол \varphi
против часовой стрелки. Следовательно, угол между прямыми FL
и AB
(точнее, тот из углов, который заключён между их лучами, сонаправленными с векторами \overrightarrow{FL}
и \overrightarrow{AB}
) равен
\angle BAC-\varphi=\alpha-\frac{1}{2}(\alpha-\gamma)=\frac{1}{2}(\alpha+\gamma),
а аналогичный угол между FL
и BC
равен
\angle ACB+\varphi=\gamma+\frac{1}{2}(\alpha-\gamma)=\frac{1}{2}(\alpha+\gamma).
Поскольку эти два угла равны, треугольник, отсекаемый прямой FL
от угла BAC
, — равнобедренный.
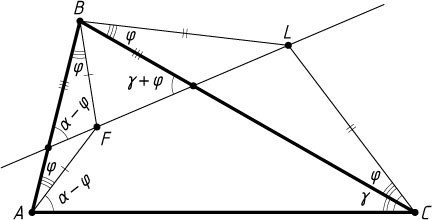
Автор: Бахарев Ф. Л.
Источник: Санкт-Петербургская (Ленинградская) математическая олимпиада. — 2004 г., отборочный тур, 9 класс
