6267. В круге проведены два перпендикулярных диаметра. Рассмотрим четыре круга, диаметрами которых служат четыре получившихся радиуса исходной окружности (см.рис.). Докажите, что суммарная площадь попарно общих частей этих кругов равна площади части исходного круга, лежащей вне рассматриваемых четырёх кругов.
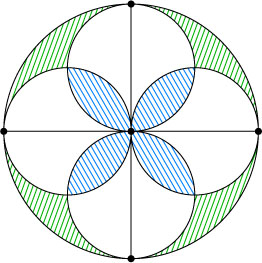
Решение. Достаточно доказать соответствующее утверждение для каждой из четырёх частей, на которые указанные диаметры разбивают исходный круг.
Рассмотрим в произвольном круге сегмент, отсекаемый хордой, стягивающей дугу в 90^{\circ}
. Пусть S
и s
соответственно — площади таких сегментов для исходного и каждого из четырёх построенных кругов. Из подобия сегментов следует, что S=4s
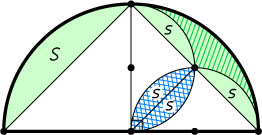
(коэффициент подобия равен 2). Остаётся заметить, что площадь части с одинарной штриховкой равна S-2s=2s
, а площадь части с двойной штриховкой равна 2s
.
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.39, с. 63
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.40, с. 61

