6271. На сторонах AB
и AC
треугольника ABC
с углом 114^{\circ}
между этими сторонами взяты точки K
и L
соответственно. Докажите, что на отрезке KL
существует такая точка O
, для которой OA\lt OB
и OA\lt OC
.
Решение. Геометрическое место точек X
, для которых XA\lt XB
есть содержащая точку A
полуплоскость, граница которой — серединный перпендикуляр к стороне AB
. Аналогично находим геометрическое место точек X
для которых XA\lt XC
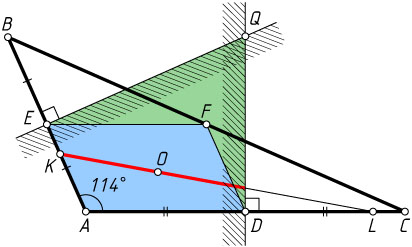
. Пересечение этих двух геометрических мест с плоским углом BAC
есть плоский четырёхугольник AEQD
(часть плоскости, ограниченная выпуклым четырёхугольником AEQD
), где D
и E
— середины сторон AC
и AB
соответственно, Q
— точка пересечения серединных перпендикуляров к сторонам треугольника, т. е. центр его описанной окружности.
Проведём средние линии DF
и EF
. Поскольку угол BAC
— тупой, точка Q
расположена вне треугольника. Тогда отрезки DF
и EF
расположены внутри четырёхугольника AEQD
. Любой отрезок KL
с концами на сторонах AB
и AC
треугольника ABC
пересекается с четырёхугольником AEQD
. Следовательно, для каждой точки O
этого отрезка, лежащей внутри четырёхугольника, верны неравенства OA\lt OB
и OA\lt OC
.
Примечание. Примером такой точки может быть точка пересечения отрезка KL
с медианой треугольника ABC
, проведённой из вершины A
, или с радиусом описанной окружности, проведённым в точку A
.