6360. В треугольнике ABC
AB=9
, BC=10
, CA=5
. Точка D
лежит на прямой BC
так, что BD:DC=3:5
. Окружности, вписанные в треугольники ADC
и ADB
, касаются стороны AD
в точках E
и F
. Найдите длину отрезка EF
.
Ответ. \frac{13}{4}
или 7.
Решение. Докажем сначала следующее утверждение. Если окружность, вписанная в треугольник KLM
, касается его стороны MK
в точке P
, то MP=\frac{1}{2}(MK+ML-KL)
.
Доказательство. Пусть Q
и R
— точки касания вписанной окружности треугольника KLM
со сторонами ML
и KL
соответственно (рис. 1). Тогда
MQ=MP,~KP=KR,~LQ=LR,
KL=KR+LR=KP+LQ=(MK-MP)+(ML-MQ)=
=MK+ML-(MP+MQ)=MK+ML-2MP.
Следовательно, MP=\frac{1}{2}(MK+ML-KL)
, что и требовалось доказать.
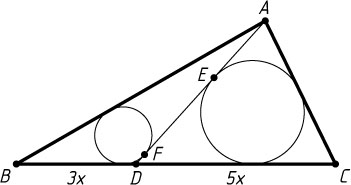
Вернёмся к нашей задаче. Пусть вписанные окружности треугольников ADC
и ABD
касаются отрезка AD
в точках E
и F
соответственно, причём точка D
лежит на отрезке BC
(рис. 2). Тогда по доказанному
AE=\frac{1}{2}(AD+AC-CD),~AF=\frac{1}{2}(AD+AB-BD),
значит,
EF=|AF-AE|=\left|\frac{1}{2}(AD+AB-BD)-\frac{1}{2}(AD+AC-CD)\right|=
=\frac{1}{2}\left|AD+AB-BD-AD-AC+CD\right|=\frac{1}{2}|AB-AC-BD+CD|=
=\frac{1}{2}\left|AB-AC-\frac{3}{8}BC+\frac{5}{8}BC\right|=\frac{1}{2}\left|AB-AC+\frac{1}{4}BC\right|=\frac{1}{2}\left|9-5+\frac{1}{4}\cdot10\right|=\frac{13}{4}.
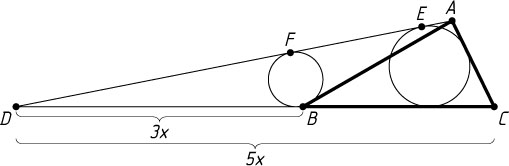
Пусть теперь точка D
лежит вне отрезка BC
(рис. 3). Тогда она лежит на продолжении отрезка BC
за точку B
. Аналогично предыдущему случаю
EF=|AF-AE|=\frac{1}{2}|AB-AC-BD+CD|=
=\frac{1}{2}\left|AB-AC-\frac{3}{2}BC+\frac{5}{2}BC\right|=\frac{1}{2}|AB-AC+BC|=\frac{1}{2}|9-5+10|=7.

Источник: ЕГЭ. — Задача C4, 2010


