6363. Основание равнобедренного треугольника равно 56, косинус угла при вершине равен \frac{7}{25}
. Две вершины прямоугольника лежат на основании треугольника, а две другие — на боковых сторонах. Найдите площадь прямоугольника, если известно, что одна из его сторон вдвое больше другой.
Ответ. 512
или 393
.
Решение. Пусть вершины K
и L
прямоугольника KLMN
лежат на основании BC
равнобедренного треугольника ABC
(точка K
между B
и L
), а вершины M
и N
— на боковых сторонах AC
и AB
соответственно.
Обозначим \angle BAC=\alpha
, \angle ABC=\angle ACB=\beta
. Тогда
\cos\alpha=\frac{7}{25},~\sin\alpha=\frac{24}{25},
\tg\beta=\tg\left(90^{\circ}-\frac{\alpha}{2}\right)=\ctg\frac{\alpha}{2}=\frac{1+\cos\alpha}{\sin\alpha}=\frac{1+\frac{7}{25}}{\frac{24}{25}}=\frac{4}{3}.
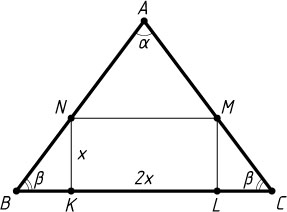
Предположим, что сторона KL
прямоугольника вдвое больше его стороны KN
(рис. 1). Положим KN=x
, KL=2x
. Из прямоугольного треугольника BKN
находим, что BK=KN\ctg\alpha=\frac{3x}{4}
. Тогда LC=BK=\frac{3x}{4}
, а так как KL=MN=2x
, то
BC=BK+KL+LC=\frac{3x}{4}+2x+\frac{3x}{4}=\frac{7}{2}x=56,
откуда x=16
. Тогда KL=2x=32
. Следовательно,
S_{KLMN}=KL\cdot KN=32\cdot16=512.
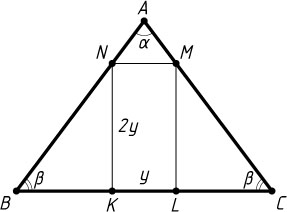
Пусть теперь сторона KN
прямоугольника вдвое больше его стороны KL
(рис. 2). Положим KL=y
, KN=2y
. Из прямоугольного треугольника BKN
находим, что BK=KN\ctg\alpha=\frac{3y}{2}
. Тогда LC=BK=\frac{3y}{2}
, а так как KL=MN=y
, то
BC=BK+KL+LC=\frac{3y}{2}+y+\frac{3y}{2}=4y=56,
откуда y=14
. Тогда KN=2y=28
. Следовательно,
S_{KLMN}=KL\cdot KN=14\cdot28=392.
Источник: Диагностические и тренировочные задачи ЕГЭ. — Задача C4, 2010

