6394. Теорема Брианшона. Докажите, что диагонали AD
, BE
и CF
описанного шестиугольника ABCDEF
пересекаются в одной точке.
Решение. Доказательство А. С. Смогоржевского. Сначала докажем следующую лемму. Если в точках P
и Q
, лежащих на окружности, провести касательные к окружности и по одну сторону от прямой PQ
отложить на них равные отрезки PP'
и QQ'
, то существует окружность, касающаяся прямых PP'
и QQ'
в точках P'
и Q'
.
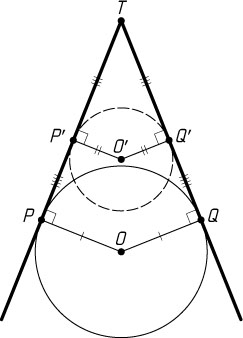
Действительно, если PP'\parallel QQ'
, доказательство очевидно. Если прямые PP'
и QQ'
пересекаются в точке T
(рис. 1), а O
— центр данной окружности, то TO
— биссектриса угла PTQ
,
TP'=TP-PP'=TQ-QQ'=TQ',
поэтому перпендикуляры к сторонам угла PTQ
, восставленные из точек P'
и Q'
, пересекаются на TO
в некоторой точке O'
, равноудалённой от сторон угла. Следовательно, O'
— центр окружности касающейся сторон угла в точках P'
и Q'
. Лемма доказана.
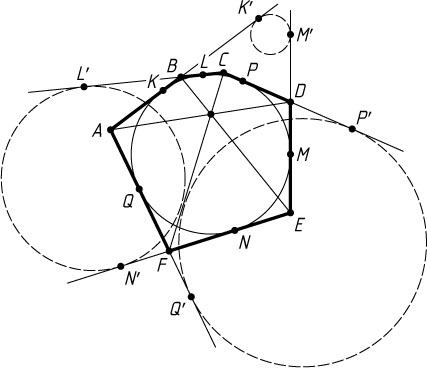
Вернёмся к нашей задаче. Пусть вписанная окружность шестиугольника ABCDEF
касается его сторон AB
, BC
, CD
, DE
, EF
и AF
соответственно в точках K
, L
, P
, M
, N
и Q
(рис. 2). На лучах AF
, CD
, AB
, ED
, EF
и CB
отложим отрезки соответственно QQ'=PP'=KK'=MM'=NN'=LL'
. По лемме существуют окружности: S_{1}
— касающаяся прямых CD
и AF
в точках P'
и Q'
, S_{2}
— касающаяся прямых AB
и ED
в точках K'
и M'
, S_{3}
— касающаяся прямых CB
и EF
в точках L'
и N'
.
Из равенств BK=BL
и KK'=LL'
следует, что BK'=BL'
, а из равенств NN'=MM'
и EN=EM
следует, что EN'=EM'
. Значит, у точек B
и E
одинаковые степени относительно окружностей S_{2}
и S_{3}
(касательные, проведённые из точек B
и E
к этим окружностям, попарно равны). Следовательно, прямая BE
— радикальная ось этих окружностей. Аналогично докажем, что прямая AD
— радикальная ось окружностей S_{1}
и S_{2}
, а прямая CF
— радикальная ось окружностей S_{1}
и S_{3}
. Поскольку центры окружностей S_{1}
, S_{2}
и S_{3}
не лежат на одной прямой, их радикальные оси пересекаются в одной точке — радикальном центре трёх этих окружностей. Что и требовалось доказать.
Примечание. Пусть окружность, вписанная в четырёхугольник ABCD
, касается его сторон AB
, BC
, CD
и CE
в точках E
, F
, G
и H
соответственно. Рассматривая этот четырёхугольник как вырожденный описанный шестиугольник AEBFCD
можно доказать, что отрезки AF
, CE
и BD
пересекаются в одной точке.
Источник: Адамар Ж. Элементарная геометрия. — Ч. 1: Планиметрия. — М.: Учпедгиз, 1948. — с. 196
Источник: Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. — Ч. 2: Геометрия (планиметрия). — М.: ГТТИ, 1952. — № 130, с. 46
Источник: Прасолов В. В. Задачи по планиметрии. — Ч. 1. — М.: Наука, 1991. — № 3.66, с. 67
Источник: Прасолов В. В. Задачи по планиметрии. — 6-е изд. — М.: МЦНМО, 2007. — № 3.73, с. 65
Источник: Коксетер Г. С. М., Грейтцер С. Л. Новые встречи с геометрией. — М.: Наука, 1978. — с. 96

